1. 서 론
2. 자 료
2.1 현장 관측 자료
2.2 위성 및 재해석 자료
2.3 입력 자료의 변환과 변수 추가
3. 기계학습 모형
3.1 Random Forest (RF)
3.2 Support Vector Machine (SVM)
3.3 Multi-Layer Perceptron (MLP)
4. 결과 및 토의
4.1 모형별 성능 비교
4.2 입력 변수 조합에 따른 RF 모형의 민감도
4.3 해양-대기 CO2 교환율 추정
5. 결 론
1. 서 론
산업 혁명 이후 인간 활동을 통해 대기로 방출된 CO2의 총량은 2011년을 기준으로 약 555 PgC (=1015 gC)으로 추정된다(Ciais et al., 2013). 해양은 이 배출량의 4분의 1 정도를 흡수함으로써, 대기 중 CO2 증가를 조절하는 역할을 하고 있다. 해양과 대기 사이 CO2 교환율(sea-to-air CO2 flux)의 시공간 변화를 정확하게 평가하는 것은 지구의 탄소순환을 이해하고, 미래 대기 CO2 농도와 기후 변화를 예측하기 위해 중요하다.
해양이 대기 CO2를 흡수하는 과정은 해양과 대기 경계면에서 기체교환을 통해 일어난다. 기체교환을 통한 CO2의 해양-대기 교환율(F, mol m-2 d-1)은 해양과 대기 fCO2(각각 (fCO2)sw와 (fCO2)air)의 차이에 비례하며, 다음 식으로 계산된다(Takahashi et al., 2009).
| $$\mathrm F=\mathrm k\cdot\mathrm s\cdot\lbrack{(f{\mathrm{CO}}_2)}_{sw}-{(f{\mathrm{CO}}_2)}_{air}\rbrack$$ | (1) |
여기서, k (m d-1)와 S (mol L-1 atm-1)는 각각 CO2의 기체교환속도와 용해도이다. k와 S는비교적 측정이 용이한 수온, 염분, 풍속으로부터 계산된다(Wanninkhof, 2014). 반면, 해양과 대기의 fCO2 (atm)는 일반적으로 대기-해수 평형기와 적외선 분석기를 결합한 시스템(Dickson et al., 2007; Pierrot et al., 2009)을 갖춘 선박을 이용하여 측정되고 있다. 상대적으로 완만한 시공간 변화를 보이는 f (CO2)air에 비해, f (CO2)sw는 해양의 물리, 생물 작용들에 의해 상당한 시공간 변화를 보이고 있어, CO2 교환율에 가장 큰 변화를 줄 수 있는 요소로 꼽힌다(Takahashi et al., 2009). 그간의 관측 결과를 종합한 최근 연구에서는 해양에 의한 CO2 교환율을 -1.6 ± 0.9 Pg-C yr-1로 보고하였다(Takahashi et al., 2009). 식 (1)의 정의에 따라 음수의 교환율은 해양에 의한 대기 CO2 흡수를 의미한다. 제한된 관측 자료로 인해, 이 연구에서는 위경도 해상도 4° x 5°로 성긴 장기평균 (fCO2)sw 분포를 제시하였다.
동해의 CO2 교환율에 대한 연구는 매우 제한적이다. Oh(1998), Oh et al.(1999)는 수온(SST), 혼합층깊이(MLD), 풍속, 생물 활동, (fCO2)air 등을 고려한 기체교환 모형을 통해 울릉분지를 포함한 동해 남부해역의 CO2 교환율을 -2.2 mol m-2 yr-1로 추정하였다. Choi et al.(2012)는 울릉분지 해역에서 2006년과 2008년에 걸쳐 계절별로 수행한 관측(총 4회)을 토대로 CO2 교환율을 -2.47 ± 1.26 mol m-2 yr-1로 추정하였다. Kim et al.(2014)은 1995년부터 2009년까지 총 14회의 현장 관측을 토대로 울릉분지 해역의 CO2 교환율을 -0.81 ± 0.49 mol m-2 yr-1(2004년 기준)로 추정하였다. 이는 이전 연구에서 제시한 교환율의 절반에 미치지 못하는 것이다. Kim et al.(2014)은 이처럼 큰 교환율 차이가 보이는 까닭을 이전 연구의 관측 횟수가 제한적이어서 울릉분지 fCO2의 큰 계절 변화를 반영하지 못하기 때문으로 해석하였다. 울릉분지의 단위 면적당 CO2 교환율(-0.81 ~ -2.47 mol m-2 yr-1)은 전세계 평균(-0.37 mol m-2 yr-1; Takahashi et al., 2009)보다 2 - 7배 가량 높다. 이 같은 관측 결과는 인간 활동에 의한 CO2 존재량(30 ~ 50 mol C m-2)이 울릉분지에서 북태평양보다 2배 가량 높게 관측되는 것과도 일치하는 것이다(Park et al., 2006).
선박을 이용한 현장관측 방법은 연구선의 운항 시기와 경로에 따라 시공간 제약을 받기 때문에, 공간 대표성이 있는 (fCO2)sw(이후 fCO2로 간략히 표현) 시계열 자료를 얻는 데 어려움이 있다. 최근 현장 관측이 갖고 있는 시공간 제약을 인공위성이나 수치 모형 자료를 이용하여 극복하고자 하는 연구가 활발히 이루어지고 있다(Telszewski et al., 2009; Nakaoka et al., 2013; Landschuster et al., 2014; Zeng et al., 2014; Gregor et al., 2017). 동해에서는 Park et al.(2016)이 처음으로 MODIS SST, CHL 자료와 위경도 정보로 인공신경망 모형을 구축하여 울릉분지 표층의 fCO2 분포와 변동성을 살펴보았다. 이 모형 결과와 현장 관측 결과의 평균제곱근오차(RMSE)는 19.2 μatm였으며, CHL보다는 SST가 fCO2와 밀접한 상관 관계를 보였다. Jang et al.(2017)은 Geostationary Ocean Color Imager (GOCI)의 해색 정보(유색 용존 유기물과 CHL 등)와 Hybrid Coordinate Ocean Model (HYCOM) 재해석 자료(수온, 염분 및 혼합층 깊이)를 입력하여 두 가지 기계학습 모형(support vector regression (SVR)과 random forest (RF))을 구축하였다. RF 모형의 경우, RMSE가 5.5 μatm으로 매우 우수한 성능을 보였다. 이 연구에서는 2015년의 CO2 교환율을 -1.53 mol m-2 yr-1로 제시하였다. 하지만 현장 관측 자료가 봄, 여름과 가을로 제한되어 있고, 모형 결과가 이전 연구에서 보였던 여름철 해양의 CO2 방출(Choi et al., 2012; Kim et al., 2014)을 보여주지 못하는 점 등에 대해서는 개선이 필요할 것으로 보인다.
본 연구에서는 이전 연구들을 통해서 수집된 현장 관측 자료(Kim et al., 2014; Park et al., 2016)와 기계학습법들을 결합하여 동해 남서부해역 표층 fCO2의 연변화를 추정하는 모형을 구축하였다. 이 모형으로 이 해역의 fCO2을 추정하는데 중요한 역할을 하는 변수가 어떤 것인가도 살펴보았다. 기계학습 모형을 통해 추정한 fCO2와 기존 연구에서 제시한 대기 fCO2를 결합하여, 동해 남서부해역 CO2 교환율을 8일 간격으로 제시하였다.
2. 자 료
2.1 현장 관측 자료
연구에 활용한 현장 관측 자료는 인공신경망기법을 이용하여 fCO2을 추정한 Park et al.(2016)의 것과 동일한 것이다. Park et al.(2016)은 이전 Kim et al.(2014)이 보고한 현장 자료(1995년부터 2009년까지) 중 MODIS-Aqua 엽록소 자료가 존재하는 2003년 이후의 관측 자료에 2011년, 2012년 관측 결과를 추가하여 연구에 활용하였다. fCO2를 비롯한 현장 관측 자료의 획득 방법은 Kim et al.(2014)을 참고하기 바란다.
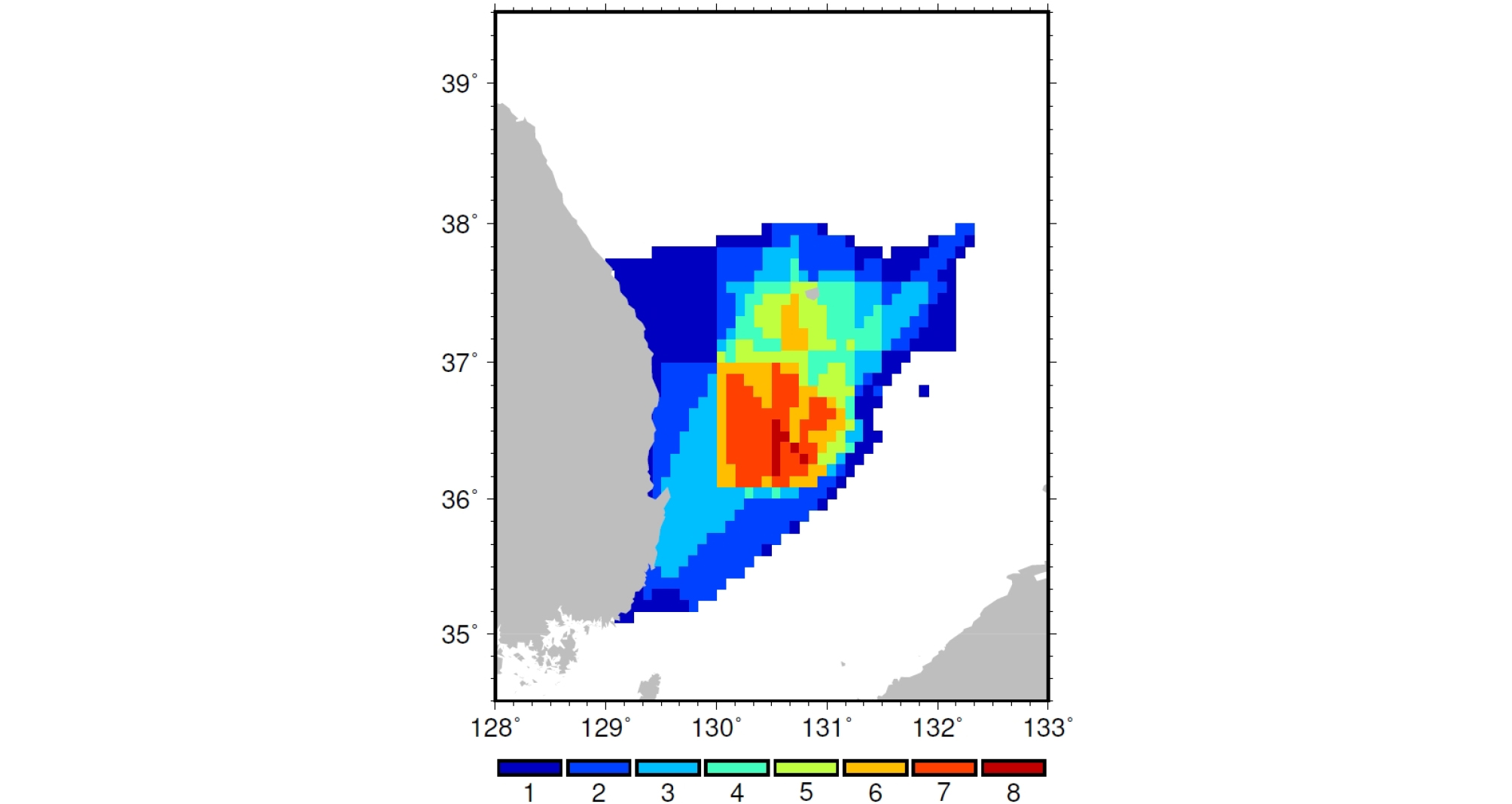
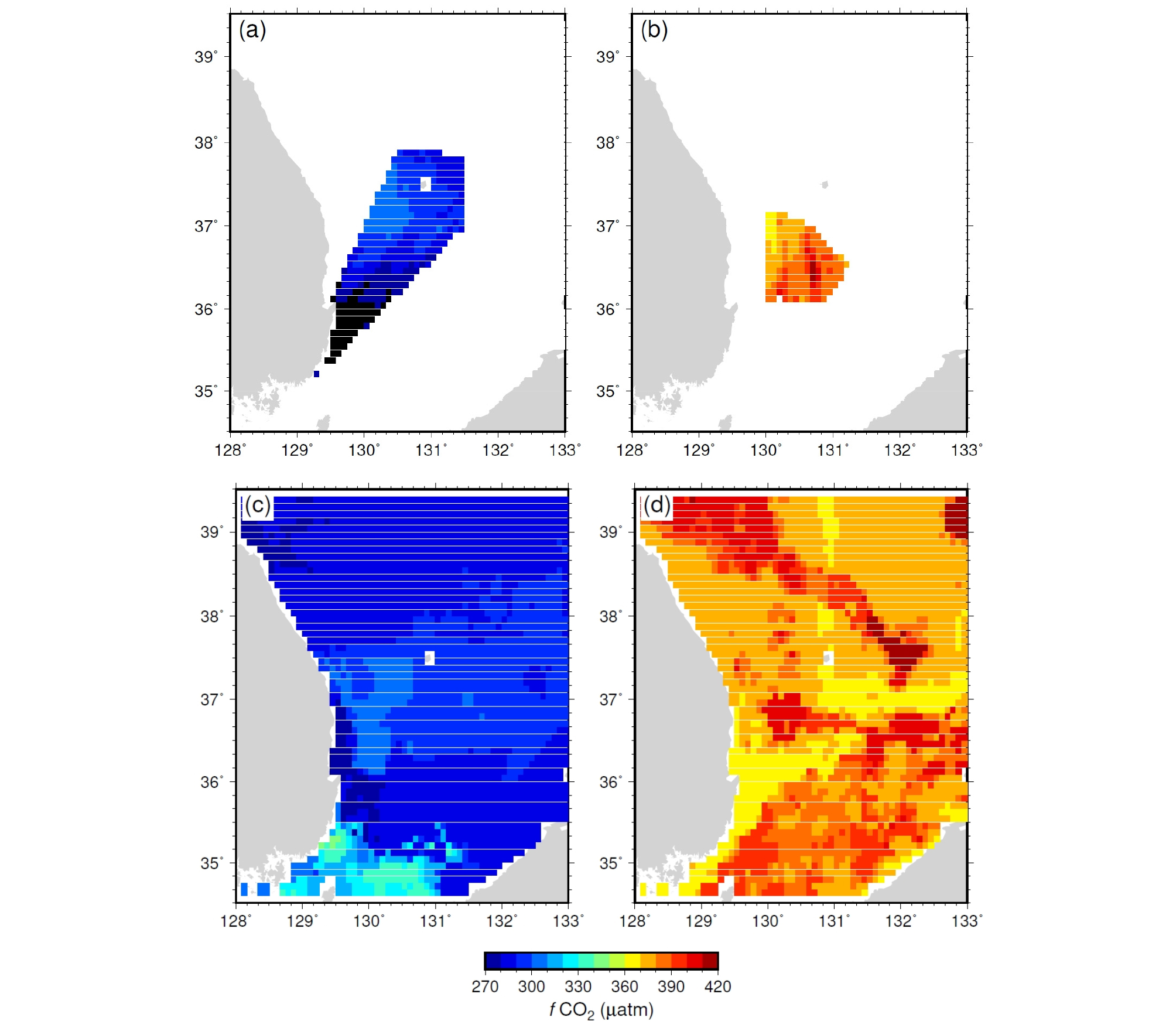
이 연구에서는 2003년부터 2012년까지 울릉분지 인근 해역에서 총 10회의 개별 탐사를 통해 얻은 17,400여개의 자료를 이용하였다. fCO2 예측을 위해 사용할 위성 혹은 재해석 자료와 시공간 해상도를 일치시키기 위해, 현장 관측 자료를 8일, 위경도 0.083° x 0.083° 간격으로 격자화하였다. 10년간 관측 결과들을 취합하였음에도 불구하고, 현장 관측자료의 갯수는 격자화 후 2,412개로 줄어들었다. 관측 빈도도 울릉분지 중앙부를 제외하고는 4회 미만으로 낮게 나타났다(Fig. 1). 제한된 현장 관측 자료로 인해 fCO2의 장기 변동을 신뢰성 있게 살펴보기 어려울 것으로 판단하여, 이 연구에서는 전체 관측 시기의 중간에 해당하는 2008년을 기준으로 fCO2 관측자료를 표준화한 후, fCO2의 연변화를 살펴보고자 하였다. 표준화에는 Kim et al.(2014)이 제시한 fCO2 증가율 2.7 μatm yr-1을 이용하였다. 즉, 2008년 이전 관측 자료들에는 2008년에 비해 평균 fCO2가 낮았던 만큼 더해 주고, 2008년 이후 관측 자료들은 2008년에 비해 높아진 fCO2만큼 빼주었다. 이를 통해 격자화한 관측 자료들의 장기 추세를 제외하고, 2008년 기준 8일 간격 fCO2 변화를 나타낼 수 있도록 하였다.
2.2 위성 및 재해석 자료
fCO2의 예측에는 표층 수온(SST), 염분(SSS), 엽록소(CHL), 혼합층깊이(MLD) 자료를 이용하였다. 이 입력 항목들은 기계학습을 이용하여 fCO2를 예측한 여러 연구에서 이용한 것과 동일하다(Nakaoka et al., 2013; Landschützer et al., 2014: Gregor et al., 2017). SST와 CHL은 MODIS-Aqua 관측 자료(R2018)를 이용하였고, SSS와 MLD는 HYCOM의 재해석 자료를 토대로 하였다(Table 1).
Table 1. Data used in the models. The spatial and temporal resolutions were set to 0.083° × 0.083° and 8 days, respectively
| SST | SSS | CHLa | MLDa | fCO2 | |
| training (testing) | in situb | in situb | MODIS-Aqua | HYCOM | in situa |
| prediction | MODIS-Aqua | HYCOM | MODIS-Aqua | HYCOM |
bFrom Kim et al. (2014) and Park et al. (2016). Refer to Table 1 of Park et al.(2016) for details.
위성을 이용한 CHL 농도 관측은 기상 조건에 따라 많은 제약이 따른다. CHL 농도 관측 자료의 빈도를 고려하여, 본 연구에 활용한 입력 자료의 시간 해상도는 8일, 위경도 해상도는 0.083°x 0.083°로 결정하였다. SST, SSS, MLD 자료는 Ocean Productivity Site (https://www.science.oregonstate.edu/ocean.productivity/)에서 얻었다. MLD는 10 m 수심에 비해 밀도가 0.03 kg m-3 증가한 수심으로 결정하였다(de Boyer Montégut et al., 2004). SSS은 일별, 0.083°x 0.083°해상도의 HYCOM 재해석 자료를 위성 자료와 동일하게 8일, 0.083°x 0.083°형태로 재격자화(산술평균)하여 사용하였다.
CO2의 해양-대기 교환율 추정에 필요한 k는 European Centre for Medium-Range Weather Forecasts (ECMWF)에서 제공하는 ERA-interim 재해석 풍속 자료를 이용하여 계산하였다. 계산에 앞서 6시간, 0.125°x 0.125°해상도의 풍속 자료를 다른 자료의 해상도와 동일하게 재격자화하였다. 풍속과 k의 상관관계는 Wanninkhof(2014)가 제시한 식을 따랐고, 앞선 연구와 비교를 돕기 위해 Wanninkhof(1992)를 이용한 계산 결과도 함께 제시하였다(Table 2).
Table 2. Estimates of Sea-to-air CO2 fluxes in the Ulleung Basin, East Sea
| Source of estimate | Year | Wind data | CO2 flux (mol m-2 yr-1) | ||
| Wanninkhof(1992) | Wanninkhof(2014) | ||||
| Oh(1998) | 1993 | Na et al.(1992) | -2.2 | - | |
| Choi et al.(2012) | 2006 - 2008 | QuikSCAT | -2.47±1.26 | - | |
| Kim et al.(2014) | 2004 | NCEP | -0.81±0.49 | - | |
| Jang et al.(2017) | 2015 | ECMWF | - | -1.53 | |
| This study | Harmonic | 2008 | ECMWF | -0.81±1.10 | -0.66±0.89 |
| RF Model 1 | 2008 | ECMWF | -0.94±1.42 | -0.76±1.15 | |
| RF Model 8 | 2008 | ECMWF | -1.08±1.40 | -0.88±1.14 | |
2.3 입력 자료의 변환과 변수 추가
기계학습 모형을 구축하기 위해 사용된 자료 중 일부는 사전 변환 과정을 거쳤다. 자료의 비대칭도(skewness)가 큰 CHL과 MLD는 정규 분포에 가까워지도록 상용로그 변환을 하였다(Nakaoka et al., 2013; Landschuster et al., 2014; Gregor et al., 2017). 경도(LON)와 위도(LAT) 자료도 기계학습 모형의 입력 자료로 활용하였다. 좌표 정보는 직접적으로 fCO2을 조절하지는 않지만, SST, SSS, CHL, MLD 등 주요 입력 자료로 설명되지 않거나, 위치에 따라 변화하는 요소들을 고려하기 위한 변수로 활용되고 있다(Nakaoka et al., 2013; Zeng et al., 2014). 자료의 계절 변화를 표현하기 위하여 날짜 순서(day of year; 이후 DOY)의 사인함수와 코사인 함수를 추가 변수로 활용하였다(Zeng et al., 2014; Gregor et al., 2017):
SDOY = sin (2 π DOY / 365)
CDOY = cos (2 π DOY / 365)
요약하면, fCO2 추정에 사용된 입력 변수는 다음과 같다.
| $$f{\mathrm{CO}}_2=f(\mathrm{SDOY},\;\mathrm{CDOY},\;\mathrm{LON},\;\mathrm{LAT},\;\mathrm{SST},\;\mathrm{SSS},\;\log_{10}(\mathrm{CHL}),\;\log_{10}(\mathrm{MLD}))$$ | (2) |
Support Vector Machine (SVM)과 Multi-Layer Perceptron (MLP) 모형을 이용한 학습과 예측에는 위 입력 변수(x)들을 추가적으로 평균(μ)과 표준편차(σ)로 표준화한 후 사용하였다(즉, (x - μ) / σ). 표준화가 필요하지 않은 Random Forest (RF) 모형에는 식 (2)의 입력 변수를 그대로 사용하였다.
3. 기계학습 모형
이 연구에서는 다양한 기계학습 모형 중 해양의 fCO2 예측에 널리 활용되고 있는 Random Forest (RF), Support Vector Machine (SVM), Multi-layer Perceptron (MLP)을 이용하여 fCO2 예측 모형을 구축하였다(Lanschuster et al., 2013; Zeng et al., 2014; Gregor et al., 2017; Jang et al., 2017). 각 모형의 구축에는 Python 기계학습 패키지인 sciki-learn을 이용하였다(https://scikit-learn.org; Pedregosa et al., 2011).
모형의 학습을 위해 앞서 기술한 격자화와 표준화 단계를 거쳐 현장 관측 자료를 준비하였다(식 (2)). 탐사별 자료의 일관성이 불분명한 CHL(엽록소 형광) 자료는 MODIS CHL 관측 자료로 대체하였고, MLD는 HYCOM 재해석 자료를 이용하였다(Table 1). 이렇게 준비한 자료 중 fCO2의 대비가 큰 봄과 가을의 자료 일부(DOY 81와 297의 자료들)는 모형이 예측한 자료를 독립적으로 검증하기 위해 먼저 분리해두었다. 이렇게 분리해 둔 자료는 511개로 전체 자료의 22%에 해당한다. 나머지 1901개의 자료 중 80%는 모형의 학습에, 20%는 학습을 마친 모형의 성능 평가에 이용하였다.
3.1 Random Forest (RF)
RF는 Decision Tree (DT)를 기본 구성 요소로 하고 있다. DT는 일련의 예/아니오 질문을 통해 자료의 분류 혹은 회귀 결정에 이르는 모형이다. DT는 비교적 이해하기 쉽고 시각화가 용이한 방법이기는 하지만, 훈련 단계에서 과적합(overfitting)하는 경향이 있어 일반화(generalization) 성능이 좋지 않다. RF는 DT 구성에 필요한 입력 자료 표본과 입력 변수(feature)를 무작위로 선택함으로써, 모두 다른 DT가 만들어지도록 한다. RF는 이 DT 결과들을 평균함으로써 DT의 과적합을 줄인다(Breiman, 2001). RF는 자료의 범위 조절이나 변수 조율에 큰 노력이 필요하지 않고, 분류와 회귀에 모두 좋은 성능을 낼 수 있어 가장 많이 이용되는 기계학습 모형 중 하나이다. 이 연구에서는 scikit-learn의 RandomForestRegressor 함수를 이용하여 모형을 구축하였다. 500개의 DT를 이용하여 결과를 산출하였으며, 다른 변수는 기본값을 사용하였다(Muller and Guido, 2017).
3.2 Support Vector Machine (SVM)
SVM은 다차원 공간에 일련의 초평면을 형성하여 분류 혹은 회귀를 수행한다. SVM은 입력 변수로 제한된 선형 공간에서 분류나 회귀가 어려운 경우에도 커널함수를 통해 다차원 공간으로 입력 자료를 재배치함으로써 효과적인 분류나 회귀 작업이 가능하도록 한다(Vapnik, 2000). SVM은 중소규모의 다양한 자료 해석에 좋은 성능을 보여주지만, 세심한 자료의 사전 준비와 변수 조율이 필요한 단점도 있다. 이 연구에서는 입력 자료를 평균 0, 분산 1로 표준화 한 후, SVM의 회귀분석 형태인 scikit-learn의 SVR 함수를 이용하여 모형을 구축하였다. 커널 함수로는 radial basis function (RBF)를 이용하였고, RBF의 최적 변수는 격자 검색 기능을 이용하여 찾았다(Muller and Guido, 2017).
3.3 Multi-Layer Perceptron (MLP)
MLP는 한 개의 입력층, 하나 혹은 복수의 은닉층(hidden layer)과 한 개의 출력층으로 이루어져 있다. 은닉층의 각 계산 단위(뉴런)에서는 상위 계산 단위의 결과들을 이용하여 가중합(weighted sum)을 계산하고, 여기에 비선형함수(tanh, relu 등)를 적용한 결과를 출력층의 가중합을 계산하는데 제공한다. 출력 결과와 참값의 차이를 계산하고, 이 차이를 줄이기 위해 계산단위 사이의 가중치를 조절(backpropagation)하는 학습 과정을 수행한다. MLP는 feed-forward neural network으로도 알려져 있으며, 앞서 소개한 Park et al.(2016)이 울릉분지 fCO2 추정을 위해 이용한 인공신경망과 동일한 방법이다(Hornik, 1991). 이 연구에서는 scikit-learn의 MLPRegressor 함수를 이용하였고, 비선형함수(tanh), 은닉층의 계산 단위 갯수(700 개) 등 최적화는 격자 검색을 통해 수행하였다(Muller and Guido, 2017).
4. 결과 및 토의
4.1 모형별 성능 비교
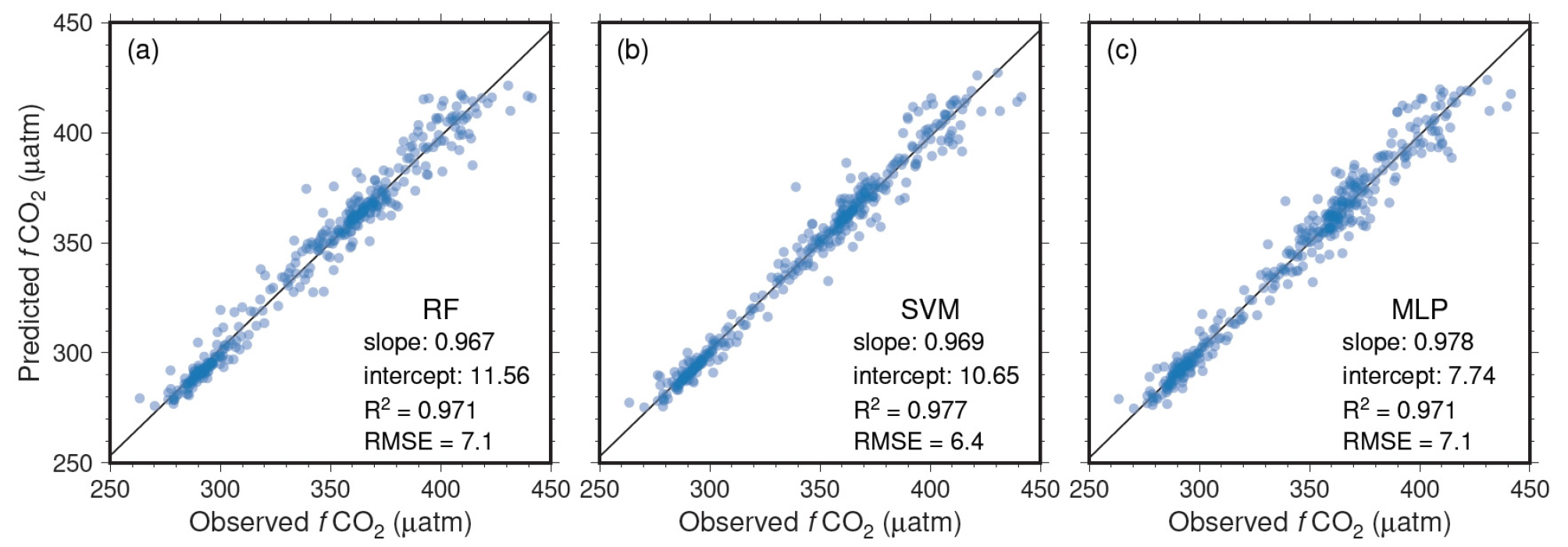
훈련을 마친 세 기계학습 모형의 성능을 비교하기 위해, 모형별로 fCO2 예측값과, 모형 시험을 위해 분리해 두었던 시험 자료의 fCO2 실측값을 비교하였다(Fig. 2). 어느 모형이나 예측값과 실측값 사이의 결정계수(coefficient of determination, R2), 평균제곱근오차(root mean square error, RMSE) 가 각각 0.97과 7 μatm 내외로 비슷한 성능을 보였다. 기울기도 1에 가까워 모든 모형이 비슷한 정도로 실측값을 잘 예측하고 있는 것을 알 수 있다.
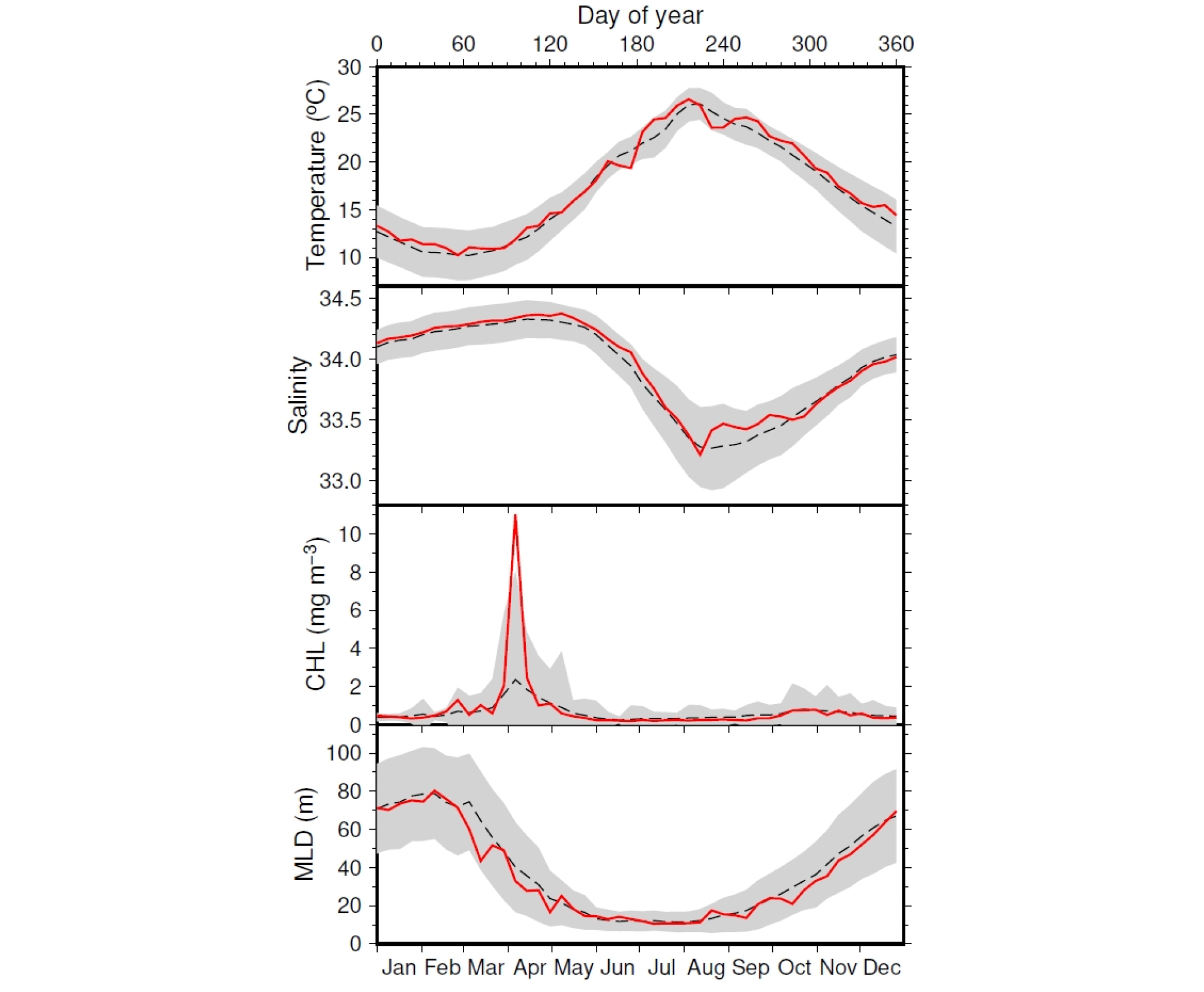
1차 시험을 마친 모형들이 fCO2의 연변화를 얼마나 잘 보여주고 있나 확인하기 위해, 모형에 2008년의 8일, 0.083° x 0.083° 해상도 자료를 입력하여 울릉분지를 포함한 동해 남서부해역(34.5 ~ 39.5°N, 128 ~ 133°E)의 fCO2를 예측하였다. 2008년 주요입력 자료의 계절변화는 장기 평균(2003년부터 2015년까지)과 대체로 유사했다(Fig. 3). CHL의 경우에는 봄 번성(4월 초) 시기에 2008년 평균이 11.0 mg m-3로 장기 평균인 2.4 mg m-3보다 현격히 높았다. 이렇게 예외적으로 높은 CHL에도 불구하고, 2008년 4월초 fCO2는 다른 해와 크게 다르진 않았다. Fig. 4에 세 모형의 8일 간격 예측 결과를 공간 평균(34.5 ~ 39.5°N, 128 ~ 133°E)하여 제시하였다. 세 모형 모두 대체로 fCO2가 봄에 최소가 되고, 여름과 겨울에 비교적 높게 나타나는 것으로 예측했다. 하지만 SVM 모형 예측에서는 봄과 겨울 사이 fCO2의 진폭이 320 ~ 360 μatm으로 매우 작게 나타났고, MLP 모형은 겨울 fCO2를 현저히 낮게 예측했다. RF 모형의 예측이 관측 결과 범위(270 ~ 420 μatm)를 가장 잘 재현했고, Kim et al.(2014)이 조화함수 형태로 제시한 fCO2의 계절 변화와도 가장 가깝게 나타났다.
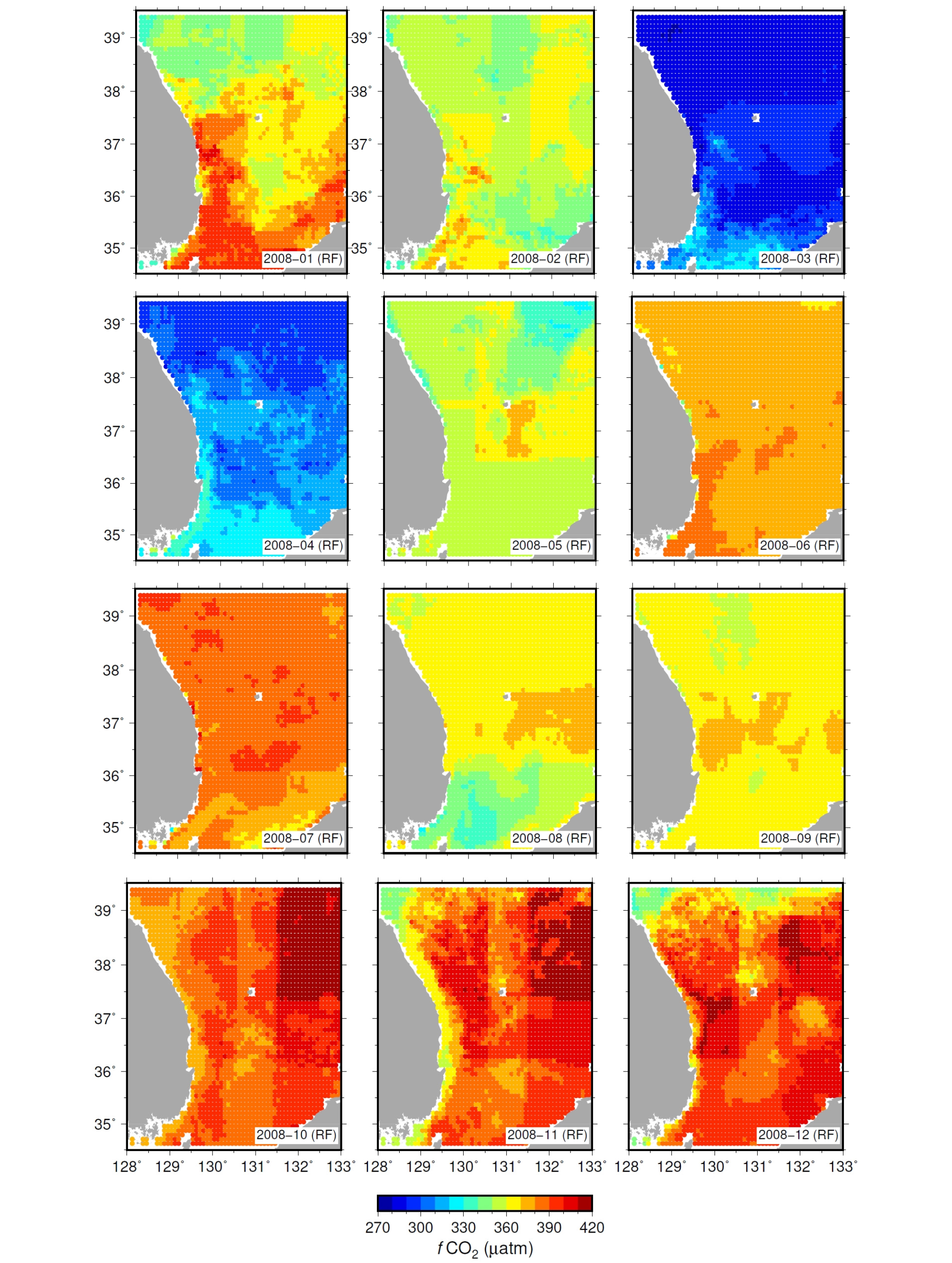
모형 검증 단계의 통계지표(결정계수와 평균제곱근오차 등; Fig. 2)로 볼 때, SVM, MLP 모형이 RF 모형과 비슷한 정도의 성능을 보임에도 불구하고, 현장 관측 결과에서 보이는 연변화를 잘 반영하지 못하는 이유는 불분명하다(Fig. 4). 다만, SVM, MLP의 월별 공간 분포를 살펴보면, 관측 자료의 빈도가 높은 울릉분지 중앙부의 fCO2 관측값과는 유사하지만, 관측 자료 빈도가 낮은 예측 범위 가장 자리의 fCO2는 과소평가하는 경향을 확인하였다. Fig. 5에 세 모형 중 가장 우수한 성능을 낸 RF 모형의 결과를 월별 평균하여 제시하였다. RF 모형은 모형의 구축과 1차 검증에 사용하지 않고 분리해두었던 현장 관측 자료(DOY 081와 297)의 시공간 분포도 대체로 잘 예측하였다(Fig. 6). 이후 입력 변수에 따른 모형의 민감도와 CO2 교환율 산출에는 RF 모형만을 이용하여 살펴보았다.
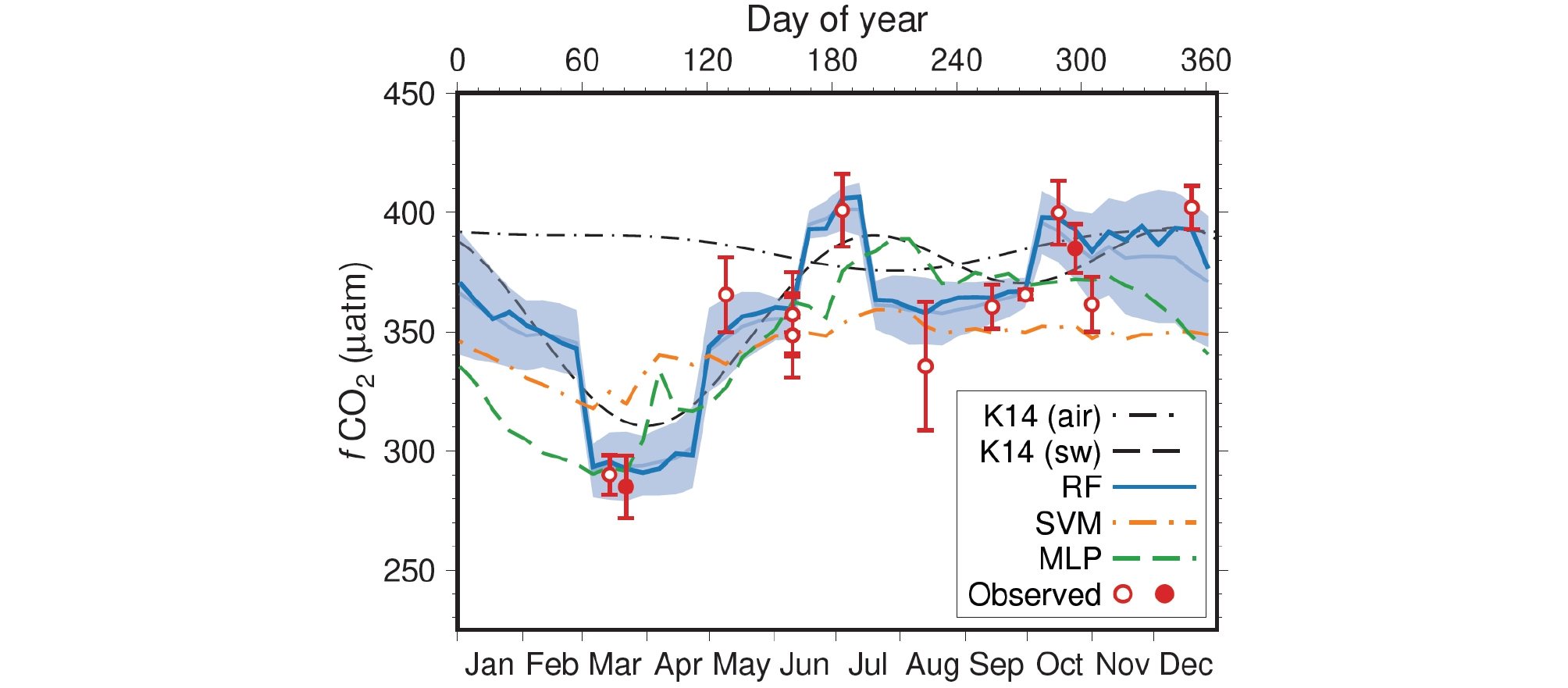
Fig. 4.
Annual variations of surface fCO2 in 2008. fCO2 variation in 2008 (dark blue line) was similar to those of the mean and standard deviation of the values in the period of 2003 - 2015 (light blue line and shade). The harmonic functions of fCO2 for the air and seawater of Kim et al. (2014) were also shown for comparison. The open circles indicate the observed data used for the construction of the models. The two solid circles (DOY 81 and 297) indicate the observed data spared for an independent comparison with the predicted values.
4.2 입력 변수 조합에 따른 RF 모형의 민감도
어떤 입력 변수가 동해 남서부해역의 표층 fCO2를 예측하는 RF 모형의 성능을 결정하는데 중요한 역할을 하는가 알아 보기 위해, 해양의 물리, 생물 해양 환경을 기술하는 기본 변수(SST, SSS, CHL, MLD), 기본 변수로 설명되지 않는 공간 변화(LON, LAT), 순환적 계절변화를 설명하기 위해 추가한 변수(SDOY, CDOY) 중 한 가지를 제외한 RF 모형들을 구축하여 성능을 비교하였다(Fig. 7a). RF 모형의 RMSE나 R2는 어느 한 변수의 제외 여부에 크게 영향을 받지 않았다. 한 변수를 제외한 모형들의 RMSE와 R2 범위는 각각 6.6 ~ 8.9 μatm, 0.955 ~ 0.975로, 모든 변수를 포함한 모형의 RMSE (7.1 μatm), R2 (0.971)와 유사하게 나타났다. 이 중 공간 좌표를 제외한 두 모형(Fig. 7의 모형 2와 9)은 다른 모형에 비해 RMSE가 25% 이상 증가하였다. 이런 결과는 연구 공간이 동해 남서부해역으로 제한되어 있지만, 기본 변수와 시간 정보만으로는 설명되지 않는 fCO2의 공간적 이질성을 일으키는 과정들이 존재함을 시사한다. 대마 난류, 여름철 감포와 울기를 중심으로 종종 일어나는 연안용승, 울릉분지에서 발견되는 에디 등이 생물생산성과 함께 fCO2의 공간 변화에 영향을 줄 수 있을 것이다(Yoo and Park, 2009; Kwak et al., 2013; Hahm et al., 2019).
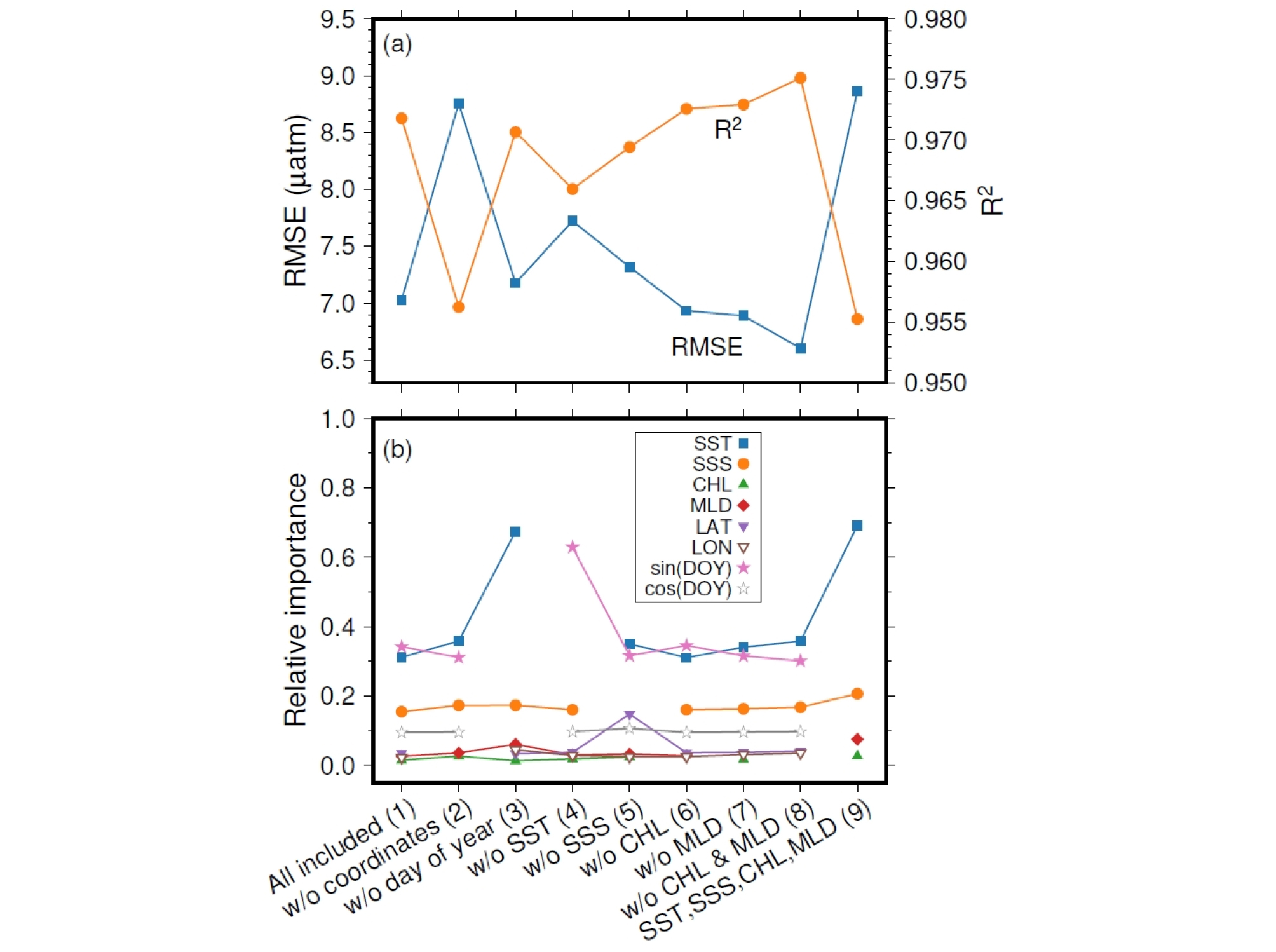
Fig. 7.
(a) Performance comparion of Random Forest (RF) models with different combinations of the input parameters. Shown are the root mean square errors (RMSE) and coefficients of determination (R2) between the observed and predicted values. (b) The variation of relative importance of an input parameter in the models fed with different combinations of the input paramters.
scikit-learn 패키지의 RF 모형 함수(RandomForestRegressor)는 개별 DT의 의사결정에 사용된 변수의 중요도(사용 빈도에 비례)를 평균함으로써 각 입력 변수의 중요도 지표(feature importance)를 제공한다. 각 변수의 중요도는 0과 1 사이의 값을 가지며, 0은 전혀 사용되지 않은 변수를, 1은 해당 변수가 완벽하게 결과를 예측함을 의미한다. 변수별 중요도의 합은 1이다. 입력 변수의 조합을 달리하였을 때, 개별 변수의 중요도 지표 변화를 Fig. 7b에 제시하였다. SST와 SDOY가 대체로 0.31 ~ 0.36로 비슷한 중요도를 갖는 것으로 나타났다. 둘 중 한 변수를 제외한 모형에서는 모형 구축에 포함된 다른 변수가 두 변수의 중요도를 합친 양에 해당하는 0.6 이상의 중요도를 보였다. 이는 SDOY가 SST의 계절 변동과 매우 유사하기 때문에, 두 변수 중 어느 하나가 제외되었을 때 다른 변수로 대부분의 fCO2 변화를 예측할 수 있음을 의미한다. SSS는 그 다음으로 높은 중요도를 갖고 있었다. fCO2를 조절하는 1차 요인이 수온, 염분에 따른 용해도 변화(Takahashi et al., 1993)인 점이 반영된 것으로 보인다.
CHL과 MLD의 중요도는 0.01 ~ 0.08로 낮게 나타났다. 공간 및 시간 정보를 제외하고 기본변수만으로 구축한 RF 모형(Fig. 7의 모형 9)에서도 SST, SSS의 중요도(각각 0.69, 0.21)에 비해 CHL과 MLD의 중요도는 0.03, 0.08로 낮았다. Kim et al.(2014)은 울릉분지 fCO2의 계절 변화를 수온 변화(‘thermal’)와 비수온 변화(‘non-thermal’)에 의한 영향으로 나눠 살펴보았다. 여기서, 비수온 변화는 생물 활동과 해수의 수직 혼합을 포함한 것이다. 저자들은 대체로 울릉분지에서 수온 및 비수온 변화에 의한 영향이 비슷하지만, 봄에는 일차생산에 의한 fCO2 감소로 인해서, 겨울에는 MLD 증가에 따라 아표층수가 표층으로 유입되어 fCO2가 증가하는 현상으로 인해서 비수온 변화의 비중이 증가한다고 보고하였다. 시간 정보가 없는 두 RF 모형의 예(Fig. 7의 모형 3과 9)에서 MLD의 상대적 중요도가 0.03에서 0.06 ~ 0.07로 증가한 점으로 볼 때, RF 모형에서는 시간 정보가 일정 부분 MLD에 따른 변화를 대변하고 있는 것으로 보인다. 입력 자료의 연변화(Fig. 3)를 살펴보면, 3월과 4월에 나타나는 CHL의 증가는 급격한 MLD의 감소와 함께 이 시기에 fCO2가 연중 최소가 되는 주요인으로 보인다. CHL과 MLD는 특정 시기에 fCO2 변화를 잘 설명하긴 하지만, RF 모형에서 fCO2의 연중 변화를 예측하는데에는 다른 변수들에 비해 중요도가 낮은 것으로 해석할 수 있겠다. CHL과 MLD를 모두 제외한 모형(Fig. 7의 모형 8)에서 미세하게나마 RMSE가 줄어들고 R2가 증가하는 것도 이런 해석을 뒷받침한다.
4.3 해양-대기 CO2 교환율 추정
RF 모형에서 추정한 해양 표층의 fCO2 분포를 이용하여 동해 남서부해역의 해양-대기 CO2 교환율을 추정하였다. 교환율 계산에 필요한 f (CO2)air의 연변화는 Kim et al.(2014)이 1995년부터 2009년까지 현장 관측 자료에 맞춰 제시한 조화함수로부터 얻었다. 앞서 소개한 8가지 변수(식 (2)) 모두를 포함한 RF 모형 1과 RMSE가 가장 작았던 RF 모형 8(CHL과 MLD 제외)은 교환율의 연변화가 매우 유사하게 나타났다(Fig. 8). 표층 fCO2가 최소인 3월과 4월을 전후하여 CO2가 가장 많이 해양으로 흡수되었고, 초여름에는 적은 양의 CO2가 대기로 방출되었다. 이 시기에 공간 변동성(파란색 음영)이 연중 가장 작은 것으로 볼 때, 전 해역에서 일관되게 CO2 방출이 일어나고 있을 것으로 추정된다. 가을에는 작은 규모의 CO2 흡수가 일어났다. 겨울철에는 교환율의 공간 변동성이 매우 큰 것으로 보아, 이 해역에서 CO2 흡수원과 방출원이 이 시기에 공존하는 것을 알 수 있다.
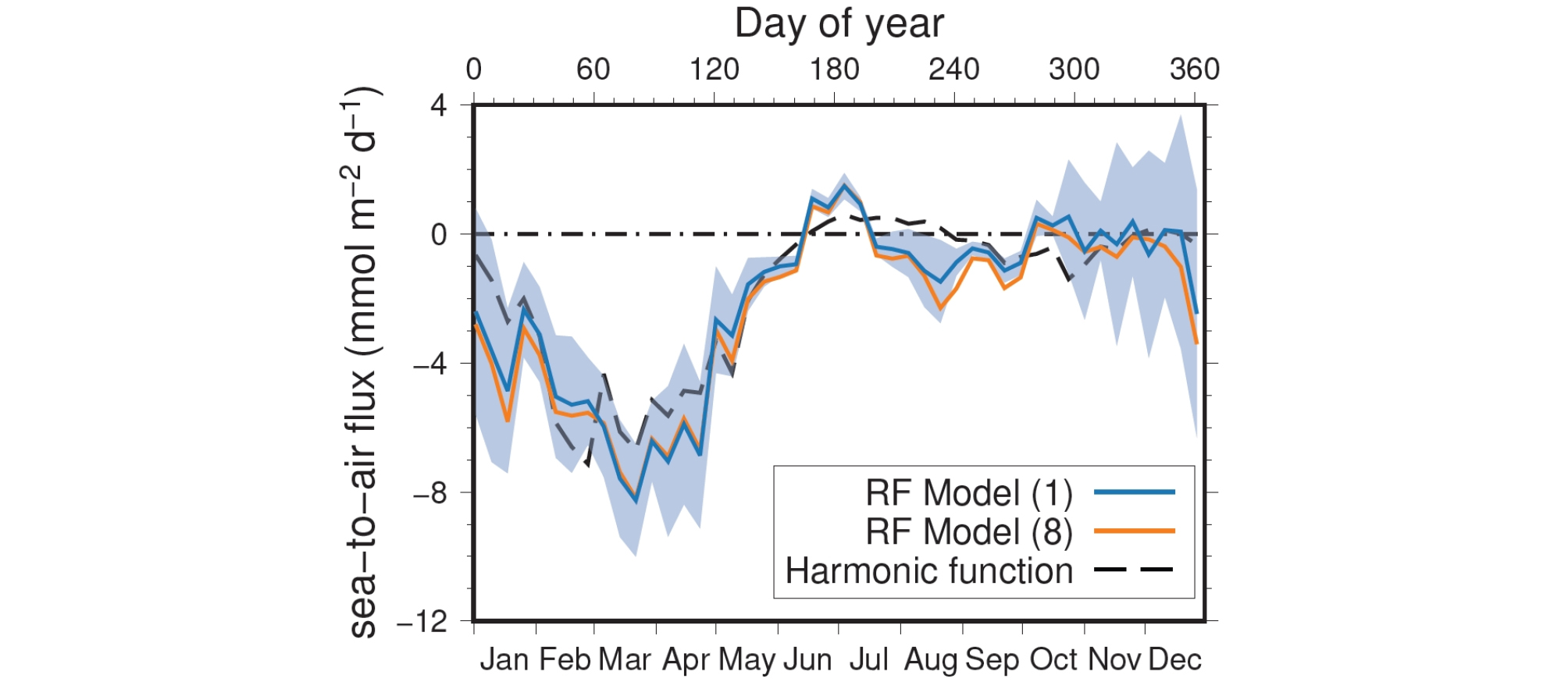
Fig. 8.
Annual variation of sea-to-air CO2 flux in the Ulleung Basin. The blue and orange lines indicate the fluxes estimated by RF Model 1 and 8 (Refer to Fig. 7 for the model numbers). The blue shade shows the standard deviations, as indicators of the spatial variability, of the fluxes estimated by RF Model 1 with 8-day interval. Also shown is the flux derived from the harmonic function of Kim et al.(2014).
RF 모형 1의 표층 fCO2 추정값을 이용하여 계산한 2008년 CO2 교환율은 -0.76±1.15 mol m-2 yr-1로, Kim et al.(2014)이 제시한 조화함수를 이용한 계산 결과 -0.66±0.89 mol m-2 yr-1보다 다소 크게 나타났다(Table 2). 이 같은 차이는 RF 모형이 조화함수보다 봄철 표층 fCO2을 조금 더 낮게 예측하고 있기 때문에 생기는 것으로 여겨진다(Fig. 4). 반대로, Jang et al.(2017)는 2015년의 교환율을 -1.53 mol m-2 yr-1로 RF 모형의 예측에 비해 2배 높게 제시하였다. 이전 연구 결과와 비교하기 위해 풍속과 기체교환속도 관계식을 Wanninkhof(2014)에서 Wanninkhof(1992)로 바꿔 계산하면, 모형 1에 의한 교환율의 크기가 -0.94±1.42 mol m-2 yr-1로 24% 가량 증가한다. 이는 Kim et al.(2014)이 2004년 교환율으로 제시한 것보다는 다소 크지만, Choi et al.(2012)이 제시한 -2.47±1.26 mol m-2 yr-1의 40%에 미치지 못하는 작은 것이다. Choi et al.(2012)은 봄과 겨울 일평균 교환율을 각각 -10.4, -13.3 mmol m-2 d-1로 제시하였다. 이는 RF 모형이나 조화함수에서 추정한 교환율의 최대 크기 -8 ~ -6 mmol m-2 d-1보다 큰 것으로 2배 이상 큰 연 교환율을 제시한 근거로 보인다. 8일 간격의 RF 모형 결과는 10일 이내의 짧은 시간에도 표층 fCO2가 상당히 변하는 것을 보여준다. 이는 정확한 CO2 교환율 추정을 위해서는 표층 fCO2가 급격하게 변하는 봄철에 현장 관측을 자주 수행하여 모형 검증에 활용할 필요가 있음을 시사한다.
5. 결 론
동해 울릉분지 해역에서는 높은 생물 생산성(Kwak et al., 2013)과 대마 난류, 연안용승, 에디 등의 물리적 요인으로 인해 fCO2가 시공간에 따라 크게 변화한다(Choi et al., 2012; Kim et al., 2014). 제한된 현장 관측 자료만으로는 파악하기 어려운 fCO2의 시공간 변화를 예측하고, 정밀한 해양-대기 CO2 교환율를 산출하기 위해, 이 연구에서는 위성 및 수치모형에서 얻은 자료들을 이용하여 기계학습 모형을 구축함으로써 동해 남서부해역의 고해상도 fCO2 시계열 자료를 얻었다. 세 모형 중 현장 관측 자료를 가장 잘 재현한 RF 모형을 이용하여 계산한 CO2 교환율은 -0.76±1.15 mol m-2 yr-1로 이전 현장 관측 연구에서 제시한 교환율(-0.66 ~ -2.47 mol m-2 yr-1) 범위 중 작은 값에 가까웠다. RF 모형이 예측한 표층 fCO2 시계열 자료는 8일 내외의 짧은 시간 사이에도 CO2 교환율에 상당한 변화가 있음을 보여주었다. 앞으로 보다 정확한 교환율 산출을 위해서는 fCO2가 급격하게 변화하는 봄철에 높은 해상도의 현장 관측을 수행할 필요가 있다. 또한, 계류시스템을 이용하여 시간 해상도가 높은 fCO2 시계열 자료를 확보할 수 있다면, 기계학습 모형에서 생산하는 fCO2 시계열 자료를 검증하는데 활용할 수 있을 것이다.