Preview
Article

The Sea Journal of the Korean Society of Oceanography. 31 May 2019. 187-207
https://doi.org/10.7850/jkso.2019.24.2.187

Development of a High Performance Ocean Model using Julia Language

줄리아 언어를 이용한 고성능 해양모델의 개발
MIN-SUN KWON1
,
JONG GU KIM1
권 민선1
,
김 종구1
1Department of Environmental Engineering, Kunsan National University
1군산대학교 환경공학과
* Corresponding Author
License (open-access):

©카피라이트

ABSTRACT

고성능 해양모델을 개발하기 위하여 적시 컴파일(Just-In-Time) 언어인 줄리아 언어를 사용하였고, 운동량 방정식의 해를 구하기 위해 연속완화법으로 푸아송 방정식을 푸는 코드를 작성하였다. 다음으로, 줄리아 계산 코드를 시험하기 위하여 두 가지의 모델을 구축하였다. 첫 번째로, 일정한 유량의 생성/소멸(source/sink) 조건을 시험하기 위해 단순한 수로 형태를 모델링하였고, 두 번째로, 조석 외력(tidal forcing) 및 전향력(Coriolis force), 난류확산계수로 인한 효과 등을 시험하기 위해 황해(Yellow Sea)를 단순화하여 모델링하였다. 모델은 두 가지 시나리오 안에서 총 8개의 실험안으로 테스트되었다. 테스트 결과, 시나리오 1에서 3가지 실험안의 수심 평균된 유속은 이론 값에 완벽하게 수렴하였고, 해저마찰로 인한 수직적 유속 구배를 잘 보여주었다. 또한 시나리오 2에서는 황해의 무조점과 우리나라 서해 중부와 남부 연안의 조석 특성을 잘 재현하였고, 전향력과 수직 난류확산계수에 따른 결과의 차이를 잘 보여주었다. 따라서, 줄리아 언어를 이용한 해양모델을 개발하는 데에 성공하였다고 판단되며, 이는 해양모델이 고전적인 컴파일 언어에서 적시 컴파일 언어로 성공적으로 넘어가는 단계에 오게 됐다는 것을 시사한다.

In order to develop a high performance ocean model, we used Julia, a Just-In-Time compile language, and to obtain the solution of the momentum equation, we made the code to solve the Poisson equation by the Successive Over-Relaxation method. And then we made two models to test Julia calculation codes. First, a simple channel form is modeled to test constant source/sink conditions. Second, the simplified Yellow Sea was modeled to test tidal forcing, Coriolis forces, and the effect of vertical eddy diffusivity coefficients. The model has been tested with a total of eight cases in the two scenarios. As a result of the test, the depth-averaged current speed of the three cases in Scenario 1 converged perfectly to the theoretical value, and that showed well a vertical flow velocity gradient due to the bottom friction. Also, the result of Scenario 2 represented well the amphidromic points of Yellow Sea and the tidal characteristics of mid-western and southwestern coast of Korea. Therefore, it is considered that the ocean model using Julia language has developed successfully, this suggests that the ocean model has come to the stage of successful transition from a classical compile language to a Just-In-Time compile language.

Keywords
Julia language
ocean modeling
Julia ocean model
hydrodynamic
Navier-Stokes Equation

MAIN

  • 1. 서 론

  • 2. 재료 및 방법

  •   2.1 기본 방정식

  •   2.2 수치해법

  •   2.3 계산 코드 작성

  •   2.4 모델 테스트를 위한 시나리오 설계

  • 3. 결 과

  •   3.1 테스트 모델 1의 결과

  •   3.2 테스트 모델 2의 결과

  • 4. 결 론

1. 서 론

과학 분야에서 수치계산에 사용되는 언어는 전통적으로 최고의 성능을 요구한다. 하지만, 전문 연구자들 중 일부는 속도가 느리더라도 이를 감내해가며 인터프리터(interpreter) 언어나 적시 컴파일(Just-In-Time compile, Aycock, 2003) 언어로써 연구를 수행하기도 한다. 이러한 언어를 즐겨 쓰는 이유는 여러 가지가 있겠지만, 가장 큰 이유는 편리함일 것이다. 예컨대, 해양학자들이 연구를 위해 해양모델링을 하려고 한다면, 대부분 컴파일 언어인 포트란으로 이루어진 모델들을 사용하게 되는데, 전처리(pre-processing)나 후처리(post-processing)에는 인터프리터 언어인 매트랩(Matlab, MathWorks, 2018)이나 파이썬(Python, Python Software Foundation, 2018) 등을 사용한다는 것이다. 기존의 해양 모델들은 매우 복잡하여 소스코드를 수정하고 컴파일하기가 쉽지 않고, 또 EFDC (Environmental Fluid Dynamic Code, Hamrick, 1992)와 같은 몇몇 모델들은 같은 포트란 언어로 작성되었다 하더라도 인텔(intel) 컴파일러 등 상용의 특정 컴파일러에서만 작동하기도 한다. 또한, 이러한 모델들은 복잡한 전처리 및 후처리 과정이 별도로 필요하며, 모델링을 위한 일련의 과정을 위하여 두 가지 이상의 언어와 툴을 별도로 익히거나 값 비싼 라이선스를 구입해야만 하는 경우도 있다. 따라서 간단한 계산이나 시뮬레이션을 위해서는 애초에 접근이 쉬운 인터프리터나 적시 컴파일 언어를 즐겨 사용하게 된다. 이러한 대화식 언어들은 전처리를 위한 데이터 파일이나 테이블 등의 처리가 수월하고, 결과의 분석과 가시화(visualization)가 용이하다. 또한, 패키지(package)나 툴 박스(tool box) 등으로 불리는 여러 가지 부 프로그램들(sub programs)의 사용이 용이하며, 이들을 이용한 확장이 자유롭다. 특히, 줄리아(Julia, JuliaLang, 2018a)나 파이썬, R (The R Foundation, 2018) 등의 언어는 플랫폼이나 환경에도 크게 구애를 받지 않고 병렬 코딩이 쉬우며 무엇보다 무료이므로, 과학자가 연구에 전념하기에 매우 유리한 조건들을 갖추고 있다. 그럼에도 불구하고, 인터프리터 언어들은 여전히 계산 속도가 아주 느리다는 치명적인 단점을 갖고 있다. 최근 적시 컴파일 방식의 도입 등으로 이러한 속도 문제가 개선되고 있기는 하나, 코딩 방식이나 최적화(optimization) 여부에 따라 속도가 천차만별로 달라질 수 있기 때문에 사용이 까다롭다.

줄리아 언어의 개발자들은 GitHub (GitHub Inc, 2018) 문서를 통해 줄리아가 ‘수치계산에 적합한 기존의 정적 타입 언어에 견줄만한 성능을 갖춘 유연한 동적 언어’라고 밝히고 있다(Julia lang., 2018b). 줄리아는 타입 추론과 LLVM (Lattner, 2002)으로 구현한 적시 컴파일을 이용하는 언어로, 파이썬, R과 같은 언어의 해석 방식과 다르다. 줄리아는 수학 프로그래밍 언어를 근간으로 탄생하였으므로 고급 단계(high level)의 수치 계산에 있어서 파이썬처럼 간편하고 표현력이 우수하다. 역사가 짧은 언어임에도 불구하고 방대한 수학 함수 라이브러리를 가지고 있기도 하다(Julia lang., 2018b). 무엇보다 GitHub에 공개된 오픈소스이므로, 줄리아 개발 커뮤니티를 통해 지속적이고 활기 있게 발전하고 있다. 줄리아 언어는 리습(lisp, McCarthy, 1960)과 유사한 매크로를 지원하고, 메타프로그래밍(meta programing)을 위한 장치들을 갖고 있다. 또한, 줄리아는 애초에 빠른 과학 컴퓨팅을 위해서 태어났으므로 병렬 처리(parallel processing)와 분산 처리(distributed processing)를 용이하게 적용할 수 있도록 고안되었다.

따라서, 본 연구에서는 이러한 줄리아 언어가 가진 장점을 바탕으로 적시 컴파일 언어로써 최고의 성능을 요구하는 해양모델을 만들고자 하였다. 해양모델을 다양한 조건에 응용하려면 모델이 고도로 복잡해지며, 실행시간이 길어진다. 이러한 이유로 연구자들이 해양모델링에 있어서는 여전히 포트란 등의 고전적인 컴파일 언어를 사용하지만, 전-후처리 과정에서 편의성이 더 높은 언어를 선호하게 되므로, 연구자들의 편의성 측면에서 매우 비효율적인 면이 있다. 그렇다고 편의성을 추구하기 위해 대화식 언어로 해양모델을 구축하고자 한다면 계산 속도가 매우 느려지는 단점이 있다. 이를 극복하기 위하여, 본 연구에서는 포트란 등의 컴파일 언어로 된 해양모델보다 훨씬 편리하고 다양한 응용이 가능하면서도 계산 속도는 포트란 언어에 근접하거나 혹은 더 빠른 줄리아 언어 기반의 고성능 해양모델을 개발하고자 하였다.

2. 재료 및 방법

2.1 기본 방정식

모델은 Arakawa-C 격자(Arakawa and Lamb, 1977)를 사용하는 완전한 3차원의 자유수면 모델로 개발되었으므로, 나비에-스톡스 식에 의해서 운동량 방정식은 아래와 같이 쓸 수 있다.

$$\frac{\partial u}{\partial t}+u\frac{\displaystyle\partial u}{\displaystyle\partial x}+\nu\frac{\displaystyle\partial u}{\displaystyle\partial y}+\omega\frac{\displaystyle\partial u}{\displaystyle\partial z}-f\nu=-\frac1{\rho_o}\frac{\partial(p+q)}{\partial x}+\frac\partial{\partial x}(A_h\frac{\partial u}{\partial x})+\frac{\displaystyle\partial}{\displaystyle\partial y}(A_h\frac{\displaystyle\partial u}{\displaystyle\partial y})+\frac{\displaystyle\partial}{\displaystyle\partial z}(A_z\frac{\displaystyle\partial u}{\displaystyle\partial z})$$ (1)
$$\frac{\displaystyle\partial\nu}{\displaystyle\partial t}+u\frac{\displaystyle\partial\nu}{\displaystyle\partial x}+\nu\frac{\displaystyle\partial\nu}{\displaystyle\partial y}+\omega\frac{\displaystyle\partial\nu}{\displaystyle\partial z}+fu=-\frac1{\rho_o}\frac{\partial(p+q)}{\partial y}+\frac\partial{\partial x}(A_h\frac{\partial v}{\partial x})+\frac{\displaystyle\partial}{\displaystyle\partial y}(A_h\frac{\displaystyle\partial v}{\displaystyle\partial y})+\frac{\displaystyle\partial}{\displaystyle\partial z}(A_z\frac{\displaystyle\partial v}{\displaystyle\partial z})$$ (2)
$$\frac{\partial\omega}{\partial t}+u\frac{\displaystyle\partial\omega}{\displaystyle\partial x}+\nu\frac{\displaystyle\partial\omega}{\displaystyle\partial y}+\omega\frac{\displaystyle\partial\omega}{\displaystyle\partial z}=-\frac1{\rho_o}\frac{\partial q}{\partial z}+\frac\partial{\partial x}(A_h\frac{\partial\omega}{\partial x})+\frac{\displaystyle\partial}{\displaystyle\partial y}(A_h\frac{\displaystyle\partial\omega}{\displaystyle\partial y})+\frac{\displaystyle\partial}{\displaystyle\partial z}(A_z\frac{\displaystyle\partial\omega}{\displaystyle\partial z})$$ (3)

여기서,

u, v, w : x, y, z 방향의 유속 성분,

f : 코리올리 파라미터(Coriolis parameter),

ρ0 : 평균 밀도(reference density),

p : 정수압(정수면으로부터의 수압),

q : 동수압(수면 경사로 인한 수압),

Ah : 수평 난류 확산 계수(m2/s),

Az : 수직 난류 확산 계수(m2/s).

비압축성 유체에서 연속 방정식은 다음과 같이 표현된다.

$$\frac{\displaystyle\partial u}{\displaystyle\partial x}+\frac{\displaystyle\partial v}{\displaystyle\partial y}+\frac{\displaystyle\partial\omega}{\displaystyle\partial z}=0$$ (4)

밀도 보존 방정식은 아래와 같이 나타낸다.

$$\frac{\displaystyle\partial\rho}{\displaystyle\partial t}+u\frac{\displaystyle\partial\rho}{\displaystyle\partial x}+v\frac{\displaystyle\partial\rho}{\displaystyle\partial y}+\omega\frac{\displaystyle\partial\rho}{\displaystyle\partial z}=\frac{\displaystyle\partial}{\displaystyle\partial x}\left(K_h\frac{\displaystyle\partial\rho}{\displaystyle\partial x}\right)+\frac{\displaystyle\partial}{\displaystyle\partial y}\left(K_h\frac{\displaystyle\partial\rho}{\displaystyle\partial y}\right)+\frac{\displaystyle\partial}{\displaystyle\partial z}\left(K_z\frac{\displaystyle\partial\rho}{\displaystyle\partial z}\right)$$ (5)

여기서,

ρ : 밀도,

Kh : 수평 난류 점성 계수(m2/s),

Kz : 수직 난류 점성 계수(m2/s).

2.2 수치해법

2.2.1 푸아송 방정식(Poisson equation)

운동방정식의 유한 차분식을 연속방정식에 대입하여 정리하면 푸아송 방정식(Poisson, 1813)이라 불리는 다음과 같은 식을 얻는다.

$$\alpha_e\triangle q_{i+1,j,k}^{n+1}+\alpha_\omega\triangle q_{i-1,j,k}^{n+1}+\alpha_n\triangle q_{i,j+1,k}^{n+1}+\alpha_s\triangle q_{i,j-1,k}^{n+1}+\alpha_t\triangle q_{i,j,k-1}^{n+1}+\alpha_b\triangle q_{i,j,k+1}^{n+1}-\alpha_0\triangle q_{i,j,k}^{n+1}=q_{i,j,k}^\ast$$ (6)

여기서, i, j, k는 각각 x, y, z의 행렬을 나타내는 지수(index)이며, n은 시간에 대한 반복계산 지수를, *표시는 연속 완화법(Successive-Over-Relaxation method) 계산을 위한 초기 추정치를 가리키며, ∆q는 동수압의 변동 값을 뜻한다. 격자 간격이 동일한 경우에 각 계수들은 아래와 같이 정리된다.

$$\alpha_e=\alpha_\omega=\frac{\triangle z_k}{\triangle x_{i,j}}$$ (7)
$$\alpha_n=\alpha_s=\frac{\triangle z_k\triangle x_{i,j}}{(\triangle y_{i,j})^2}$$ (8)
$$\alpha_t=\alpha_b=\frac{\triangle x_{i,j}}{\triangle z_k}$$ (9)
$$\alpha_0=2\times\left(\frac{\triangle z_k}{\triangle x_{i,j}}+\frac{\triangle z_k\triangle x_{i,j}}{(\triangle y_{i,j})^2}+\frac{\triangle x_{i,j}}{\triangle z_k}\right)$$ (10)

여기서, ∆x,∆y,∆z는 각각 x, y, z 방향의 격자 간격이며, 위 식에서 우변은 아래와 같이 정리된다.

$$q_{i,j,k}^\ast=\frac{\rho_0}{\triangle t}\left[(u_{i,j,k}^\ast-u_{i-1,j,k}^\ast)\triangle z_k+(v_{i,j,k}^\ast-v_{i,j-1,k}^\ast)\frac{\triangle x_{i,j}\triangle z_k}{\triangle y_{i,j}}+(\omega_{i,j,k}^\ast-\omega_{i,j,k+1}^\ast)\triangle x_{i,j}\right]$$ (11)

여기서, ∆t는 계산 시간간격을 뜻한다. ui,j,k*,vi,j,k*,wi,j,k*는 식 (1)~(3)의 유한 차분 식으로부터 계산되는 초기추정치로, 아래와 같이 코리올리 힘과 압력, 이류, 확산에 의한 유속 성분들의 합으로 나타낼 수 있다.

$$u_{i,j,k}^\ast=\cos(\alpha)u_{i,j,k}^n+\sin(\alpha)\nu_u^n-\triangle t(Ad\nu(u))+\triangle t(-\frac1{\rho_0\triangle x}(p_{i,j,k+1}^n-p_{i,j,k}^n+q_{i,j,k+1}^n-q_{i,j,k}^n)+Diff(u))$$ (12)
$$v_{i,j,k}^\ast=\cos(\alpha)v_{i,j,k}^n+\sin(\alpha)u_v^n-\triangle t(Ad\nu(v))+\triangle t(-\frac1{\rho_0\triangle y}(p_{i,j+1,k}^n-p_{i,j,k}^n+q_{i,j+1,k}^n-q_{i,j,k}^n)+Diff(v))$$ (13)
$$\omega_{i,j,k}^\ast=\omega_{i,j,k}^n-\triangle t(Adv(\omega))+\triangle t(-\frac1{\rho_0\triangle z}(q_{i-1,j,k}^n-q_{i,j,k}^n)+Diff(\omega))$$ (14)

여기서, cos(α)ui,j,kn+sin(α)vun 및 cos(α)vi,j,kn-sin(α)uun는 식 (28), (29)에 기술한 전향력의 유한 차분식이며, uv, vuvu는 각각 v와 u 격자점으로 내삽된 u, v 값이다. 또한, Adv(u), Adv(v), Adv(w)는 식 (32)~(34)로 기술된 비선형 이류항의 유한 차분식을 가리키며, Diff(u), Diff(v), Diff(w)는 식 (53)~(55)로 기술된 운동량 확산항의 유한 차분식을 가리킨다.

2.2.2 연속 완화법(Successive Over Relaxation method)

푸아송 방정식은 아래와 같이 연속 완화법으로 반복하여 풀 수 있다.

$$\triangle q_{i,j,k}^{r+1}=(1-\omega)\triangle q_{i,j,k}^r+\frac\omega{\alpha_0}(-q_{i,j,k}^\ast+\alpha_t\triangle q_{i,j,k-1}^r+\alpha_b\triangle q_{i,j,k+1}^r+\alpha_\omega\triangle q_{i-1,j,k}^r+\alpha_e\triangle q_{i+1,j,k}^r+\alpha_s\triangle q_{i,j-1,k}^r+\alpha_n\triangle q_{i,j+1,k}^r)$$ (15)

여기서, r은 반복계산(iterations)의 횟수를 의미하고, ω는 완화변수(relaxation parameter)로 0에서 2 사이의 값을 가지며, 본 연구에서는 1.4의 값을 취하였다. 초기조건으로부터 위 식을 계산하여 ∆qi,j,kr+1을 구하는 것이 1단계이며, 2단계 계산은 위의 식 (12)~(14)의 좌변을 계산하여 다음 시간 단계의 유속 추정치 ui,j,kn+1,vi,j,kn+1,wi,j,kn+1를 구하는 것이다. 또한, 3단계로서 수직 층의 수가 nk일 때, 아래와 같이 연직 적분된 수평 유속 성분을 구한다.

$$U_{i,j}^{n+1}=\sum_{k=1}^{nk}(u_{i,j,k}^{n+1}\triangle z_k)$$ (16)
$$V_{i,j}^{n+1}=\sum_{k=1}^{nk}(v_{i,j,k}^{n+1}\triangle z_k)$$ (17)

마지막 4단계로 위에서 구한 수평 유속성분을 이용해 아래와 같이 동수압 변동을 계산하면 1회의 반복 계산이 끝난다.

$$\triangle q_{i,j,0}^{r+1}=-\triangle t\times\rho_0\times g\times\left[(U_{i,j}^{n+1}-U_{i-1,j}^{n+1})/\triangle x+(V_{i,j}^{n+1}-V_{i,j-1}^{n+1})/\triangle y\right]$$ (18)

위 4단계 과정은 다음 조건이 만족될 때까지 계속된다.

$$\left|\triangle q_{i,j,k}^{r+1}-\triangle q_{i,j,k}^r\right|<\in$$ (19)

여기서, ∈은 동수압의 정확도로서, 수면 변동과는 ∆η≈∈gρ0의 관계를 가진다. 이 4 단계로 구성된 연속완화법 반복계산이 해양모델에서 가장 복잡하고 계산 시간을 가장 많이 소요하는 루프가 된다. 계산 시간을 줄이기 위해서는 코드가 잘 최적화되어야 한다. 줄리아와 같은 적시 컴파일 언어들은 최적화 문제를 늘 동반한다. 줄리아 언어가 과학 계산의 용도로 개발되었으나, 이는 어디까지나 최적화가 잘 되었을 때에 해당하는 것이다. 계산 코드의 최적화 성패 여부에 따라 모델의 계산 성능은 수 배에서 수만 배까지 차이가 날 수 있다.

2.2.3 전향력

식 (12)와 (13)의 우변에 있는 전향력의 해법은 반음해법(semi-implicit method)을 사용하는 것이 일반적이다. 우선, 식 (1)과 (2)의 운동방정식에서 전향력만 고려하면 식은 아래와 같이 간단해진다.

$$\frac{\partial u}{\partial t}-fv=0$$ (20)
$$\frac{\partial v}{\partial t}-fu=0$$ (21)

이는 아래의 유한 차분식으로 나타낼 수 있다.

$$u^{n+1}-u^n=+\triangle tfv^n$$ (22)
$$v^{n+1}-v^n=+\triangle tfu^n$$ (23)

위 식을 α=∆tf로 두고, 반음해법으로 정리하면 아래와 같다.

$$u^{n+1}=u^n+0.5\alpha(v^n+v^{n+1})$$ (24)
$$v^{n+1}=v^n-0.5\alpha(u^n+u^{n+1})$$ (25)

위 식에서 우변의 분모와 분자에 각각 0.5α를 곱하고 식 (24)와 (25)를 서로 대입하여 정리한 후 β=(0.5α)2로 두면, 아래와 같이 정리할 수 있다.

$$u^{n+1}=\frac{(1-\beta)u^n+\alpha v^n}{1+\beta}$$ (26)
$$v^{n+1}=\frac{(1-\beta)v^n-\alpha u^n}{1+\beta}$$ (27)

한편, 전향력은 겉보기 힘으로 항상 운동방향에 수직으로 작용하므로, 국지적 회전 효과로 접근하여 아래와 같은 방법으로 나타낼 수도 있다(Kämpf, 2009).

$$u^{n+1}=\cos(\alpha)u^n+\sin(\alpha)\nu^n$$ (28)
$$v^{n+1}=\cos(\alpha)v^n-\sin(\alpha)u^n$$ (29)

여기서, 회전각은 α=2×arcsin(0.5∆tf) 이다. y=2×arcsin(x/2)의 그래프는 x 값이 1보다 작아질 때부터는 거의 y 값과 같아지며, ∆tf는 일반적으로 1보다 매우 작기 때문에, α=∆tf로 근사할 수 있다. 이를 이용해 계산 코드를 더욱 간소화할 수 있으며, 식 (26), (27)의 반음해법과 식 (28), (29)의 계산 결과는 동일하다. 또한, 기본적으로 본 연구에서는 전향력을 β-plane으로 적용하는데, 이는 y 방향으로의 거리에 따라 코리올리 파라미터(f)가 다음과 같이 변하는 것을 뜻한다.

$$f=f_0+\beta y$$ (30)

여기서, β=2.22×10-11m-1s-1 이며, f0=1×10-4/s, y는 y 방향으로의 누적 거리를 나타낸다.

2.2.4 이류항의 처리

이류되는 대상을 B라 할 때, 이류 방정식은 다음과 같이 표현된다. 비선형 운동량 이류식의 경우에 B는 각각 u, v, w가 된다.

$$\frac{\partial B}{\partial t}=\frac{\displaystyle\partial(uB)}{\displaystyle\partial x}-\frac{\displaystyle\partial(vB)}{\displaystyle\partial y}-\frac{\displaystyle\partial(\omega B)}{\displaystyle\partial z}+B(\frac{\displaystyle\partial u}{\displaystyle\partial x}+\frac{\displaystyle\partial v}{\displaystyle\partial y}+\frac{\displaystyle\partial\omega}{\displaystyle\partial z})$$ (31)

위 식은 육면체 컨트롤 볼륨(control volume)의 각 면을 통한 플럭스(flux)를 이용하여 나타낼 수 있다.

$$-\triangle t\frac{\partial(uB)}{\partial x}=C_\omega^+B_\omega^++C_\omega^-B_\omega^--C_e^+B_e^+-C_e^-B_e^-$$ (32)
$$-\triangle t\frac{\partial(vB)}{\partial y}=C_s^+B_s^++C_s^-B_s^--C_n^+B_n^+-C_n^-B_n^-$$ (33)
$$-\triangle t\frac{\partial(\omega B)}{\partial z}=C_t^+B_t^++C_t^-B_t^--C_b^+B_b^+-C_b^-B_b^-$$ (34)

위 식에서, C는 컨트롤 볼륨의 각 여섯 면의 쿠랑 수(Courant number)로, 각각의 면에 대하여 아래와 같이 정의된다.

$$C_\omega^+=u_{i-1}^+\frac{\triangle t}{\triangle x},\;\;C_\omega^-=u_{i-1}^-\frac{\triangle t}{\triangle x},\;\;C_e^+=u_i^+\frac{\triangle t}{\triangle x},\;\;C_e^-=u_i^-\frac{\triangle t}{\triangle x}$$ (35)
$$C_s^+=v_{j-1}^+\frac{\triangle t}{\triangle y},\;\;C_s^-=v_{j-1}^-\frac{\triangle t}{\triangle y},\;\;C_n^+=v_j^+\frac{\triangle t}{\triangle y},\;\;C_n^-=u_j^-\frac{\triangle t}{\triangle y}$$ (36)
$$C_b^+=\omega_{k+1}^+\frac{\triangle t}{\triangle z},\;\;C_b^-=\omega_{k+1}^-\frac{\triangle t}{\triangle z},\;\;C_t^+=\omega_k^+\frac{\triangle t}{\triangle z},\;\;C_t^-=\omega_k^-\frac{\triangle t}{\triangle z}$$ (37)

여기서,

$$u^+=0.5\;(u+\left|u\right|),\;u^-=0.5\;(u-\left|u\right|)$$
$$v^+=0.5\;(v+\left|v\right|),\;v^-=0.5\;(v-\left|v\right|)$$
$$w^+=0.5\;(w+\left|w\right|),\;w^-=0.5\;(w-\left|w\right|)$$

이류항의 계산에 있어서는 TVD (Total Variation Diminishing) 기법(Fringer et al., 2005)을 도입하였다. TVD 기법은 컨트롤 볼륨에서 각 면에서의 변수 B의 값은 상류 값에 제한함수의 영향을 받는 고차항을 추가하여 계산하는 방식으로 아래와 같이 나타낼 수 있다.

$$B_\omega^+=B_{i-1}+0.5\Psi(r_{i-1}^+)(1-C_\omega^+)(B_i-B_{i-1})$$ (38)
$$B_\omega^-=B_i-0.5\Psi(r_{i-1}^-)(1+C_\omega^-)(B_i-B_{i-1})$$ (39)
$$B_e^+=B_i+0.5\Psi(r_i^+)(1-C_e^+)(B_{i+1}-B_i)$$ (40)
$$B_e^-=B_{i+1}+0.5\Psi(r_i^+)(1+C_e^-)(B_{i+1}-B_i)$$ (41)
$$B_s^+=B_{j-1}+0.5\Psi(r_{j-1}^+)(1-C_s^+)(B_j-B_{j-1})$$ (42)
$$B_s^-=B_j-0.5\Psi(r_{j-1}^+)(1+C_s^-)(B_j-B_{j-1})$$ (43)
$$B_n^+=B_j+0.5\Psi(r_j^+)(1-C_n^+)(B_{j+1}-B_j)$$ (44)
$$B_n^-=B_{j+1}-0.5\Psi(r_j^-)(1+C_n^-)(B_{j+1}-B_j)$$ (45)
$$B_b^+=B_{k+1}+0.5\Psi(r_{k+1}^+)(1-C_b^+)(B_k-B_{k+1})$$ (46)
$$B_b^-=B_k-0.5\Psi(r_{k+1}^-)(1+C_b^-)(B_k-B_{k+1})$$ (47)
$$B_t^+=B_k+0.5\Psi(r_k^+)(1-C_t^+)(B_{k-1}-B_k)$$ (48)
$$B_t^-=B_{k-1}-0.5\Psi(r_k^-)(1+C_t^-)(B_{k-1}-B_k)$$ (49)

위 식에서, 계수 r은 각각 다음과 같이 정의한다.

$$r_i^+=\frac{B_i-B_{i-1}}{B_{i+1}-B_i},\;\;r_i^-=\frac{B_{i+2}-B_{i+1}}{B_{i+1}-B_i}$$ (50)
$$r_j^+=\frac{B_j-B_{j-1}}{B_{j+1}-B_j},\;\;r_j^-=\frac{B_{j+2}-B_{j+1}}{B_{j+1}-B_j}$$ (51)
$$r_k^+=\frac{B_k-B_{k+1}}{B_{k-1}-B_k},\;\;r_k^-=\frac{B_{k-2}-B_{k-1}}{B_{k-1}-B_k}$$ (52)

마지막으로, 위 식 (38)~(49)에서 제한함수(ψ)가 0이면, 상류기법(upstream scheme), 1이면 렉스-웬드로프 기법(Lax-Wendroff scheme), 0≦ψ(r)≦2 의 경우에는 본 연구에서 채택한 슈퍼비 기법(Super-B scheme)이 된다.

2.2.5 확산항의 처리

운동량 u, v, w를 ψ라 할 때, 운동량 확산의 유한 차분식은 양해법으로 아래와 같이 쓸 수 있다.

$$\frac\partial{\partial x}\;\left(A_h\frac{\partial\psi}{\partial x}\right)=\frac{A_h^e\left(\psi_{i+1,j,k}-\psi_{i,j,k}\right)-A_h^w\left(\psi_{i,j,k}-\psi_{i-1,j,k}\right)}{\displaystyle\left(\triangle x\right)^2}$$ (53)
$$\frac\partial{\partial y}\;\left(A_h\frac{\partial\psi}{\partial y}\right)=\frac{A_h^n\left(\psi_{i,j+1,k}-\psi_{i,j,k}\right)-A_h^s\left(\psi_{i,j,k}-\psi_{i,j-1,k}\right)}{\displaystyle\left(\triangle y\right)^2}$$ (54)
$$\frac\partial{\partial z}\;\left(A_z\frac{\partial\psi}{\partial z}\right)=\frac{A_z^t\left(\psi_{i,j,k-1}-\psi_{i,j,k}\right)-A_z^b\left(\psi_{i,j,k}-\psi_{i,j,k+1}\right)}{\displaystyle\left(\triangle z\right)^2}$$ (55)

여기서,

Ahe,Ahw,Ahn,Ahs : 컨트롤 볼륨의 동서남북 방향 각 면에서의 수평 난류 확산 계수

Azt,Azb : 컨트롤 볼륨의 위·아래 방향 각 면에서의 수직 난류 확산 계수

위 확산항에 곱해지는 수평, 수직 난류확산계수(Ah,Az)는 난류 마감 기법(turbulence closure scheme)에 의해 계산된다. 수직 난류 확산과 난류 점성은 Kochergin(1987)의 개선된 난류 모델(advanced turbulence model)을 이용하였다.

$$A_z=\left(0.15\times\triangle z\right)^2\;\sqrt{\left(\frac{\partial u}{\partial z}\right)^2+\left(\frac{\partial v}{\partial z}\right)^2-N^2}$$ (56)

여기서, N2은 브런트-바이살라 주파수(Brunt, 1927; Väisäla, 1925)로 아래와 같다.

$$N^2=-g\rho_0\times\frac{\left(\rho_{i,j,k-1}-\rho_{i,j,k+1}\right)}{2\triangle z_k}$$ (57)

수평 난류 확산과 난류 점성은 Smagorinsky(1963)의 난류 모델을 사용하였다.

$$A_h=\left(c_1\times\triangle x\triangle y\right)\;\sqrt{\left(\frac{\partial u}{\partial x}\right)^2+\left(\frac{\partial v}{\partial y}\right)^2+0.5\;\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)^2+}c_2$$ (58)

여기서, c1은 무차원 난류확산계수이며, c2 배경 상수(background constant)이다.

한편, 해저마찰은 운동량 확산항에서 처리되는데, x, y방향의 해저 마찰항(τxρ0,τyρ0)은 바닥에 가장 가까운 셀에서 다음의 2차식으로 계산된다.

$$\frac{\tau_x}{\rho_0}=ru\sqrt{u^2+v^2}$$ (59)
$$\frac{\tau_y}{\rho_0}=rv\sqrt{u^2+v^2}$$ (60)

마찰계수 r은 무차원수이며, 시나리오 1에서는 r 값을 0, 0.1, 0.2로 바꿔가며 실험한 후 결과를 비교하였고, 시나리오 2에서는 r 값을 0.0015로 고정하였다. 바닥층에서 식 (55)는 다음과 같이 마찰항을 포함한 식이 된다.

$$\frac\partial{\partial z}\;\left(A_z\frac{\partial u}{\partial z}\right)=\left(A_z^t\frac{\left(u_{i,j,k-1}-u_{i,j,k}\right)}{\displaystyle\left(\triangle z\right)^2}-\frac{\tau_x}{\rho_0\triangle z}\right)$$ (61)
$$\frac\partial{\partial z}\;\left(A_z\frac{\partial v}{\partial z}\right)=\left(A_z^t\frac{\left(v_{i,j,k-1}-v_{i,j,k}\right)}{\displaystyle\left(\triangle z\right)^2}-\frac{\tau_y}{\rho_0\triangle z}\right)$$ (62)

2.3 계산 코드 작성

줄리아 계산 코드는 총 12개의 파일(files), 1개의 메인 프로그램(main program), 16개의 함수(function)로 작성되었다. 각 계산식들의 알고리즘은 Kämpf(2010)의 오픈 소스 포트란 알고리즘을 참고하여 작성하였으며, 소스코드는 GitHub (julia_ocean_model)에 공개하였다. 줄리아 코드와 포트란 코드의 가장 큰 차이는, 줄리아 코드의 경우 최적화 문제 때문에 전역 변수를 많이 사용하지 않았다는 것이며, 포트란에서 서브루틴으로 처리한 알고리즘들이 줄리아 코드에서는 함수의 형태로 동적으로 처리된다는 것이다. Table 1은 모델 개발을 위해 작성된 줄리아 코드의 구성과 내용을 요약한 것이다.

포트란 코드는 전역 변수를 사용하지만, 줄리아 언어는 전역 변수를 사용하지 않음으로써 계산 속도를 향상시킬 수 있다. 변수를 선언하는 방법은 전역 변수의 사용과 크게 다르지 않은데, 최적화를 위해서는 변수의 크기를 할당해주고 각 함수들을 호출할 때 필요한 변수들을 넘겨주고 넘겨받는 방식으로 사용한다. 만약, 잘못된 타입 선언이나 적절한 곳으로 변수를 전달해주지 못한다면 최적화에 실패하고 계산 시간이 급수적으로 늘어나게 되는데, 이를 해결하기 위해서는 @time 매크로를 이용해 메모리와 계산 시간을 가장 많이 소요하는 프로세스를 찾고, 이러한 프로세스들이 왜 시간을 많이 소요하는지 이해한 다음, 변수들의 수와 크기 등을 고려하여 최적화해야 한다.

Table 1. Julia model files and contents

No. Contents Julia codes
File Name Type
1 Topography reading and main loop readtopo.jl 1 function
2 Initializing variables JOM.jl program
Forcing and dynamic calculate
3 Vertical turbulence model eddyVertical.jl 1 function
4 Horizontal turbulence model eddyHorizontal.jl 1 function
5 Advection advection.jl 2 functions
6 Density density.jl 1 function
7 Hydrostatic hydrostatic.jl 1 function
8 u,v,w momentum advection momentadv.jl 1 function
9 u,v,w momentum diffusion momentdif.jl 1 function
10 Surface wind shear stress surfaceWindShear.jl 1 function
11 Bottom shear stress bottomShear.jl 1 function
12 Poisson equation and S.O.R. iterations poisson.jl 8 function

2.4 모델 테스트를 위한 시나리오 설계

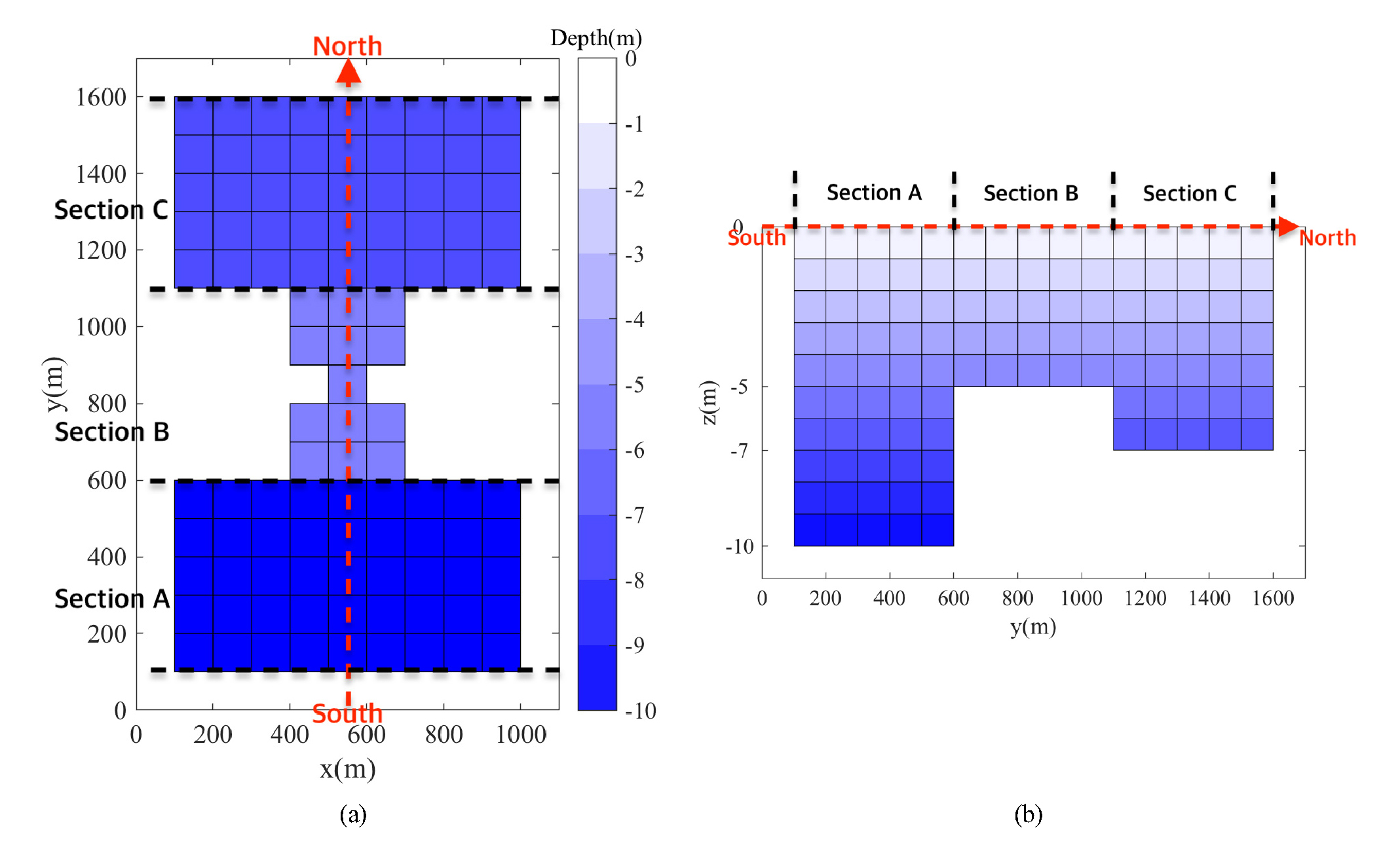
줄리아 계산 코드를 시험하기 위하여 두 가지의 모델을 구축하였다. 첫 번째로, 일정한 유량의 생성/소멸(source/sink) 조건을 시험하기 위해 단순한 수로 형태를 모델링하였다. x 방향으로 9개, y 방향으로 15개, z 방향으로 10개의 격자를 생성하였고, x, y 방향의 격자 간격은 100 m, z 방향의 격자 간격은 1 m로 구성하였다. 수심은 Fig. 1과 같이 임의로 3개의 섹션을 나누어 각각 A는 10 m, B는 5 m, C는 7 m 로 설정하였다. 섹션마다 수심을 다르게 한 이유는, 단지 모델이 급격한 수심변화에 잘 대처하는지 보고자 함이다. 경계조건은 닫힌 경계의 직교 방향에 대해서 반 미끄러짐(semi-slip) 조건을 적용하였고, 개방 경계에 대해서는 유량의 생성/소멸로 인한 동수압 q의 변동을 디리클레 조건(dirichlet condition)으로 입력하였다. 모델의 계산 시간 간격은 2초이며, 1일간 모의하였고, 결과의 출력 간격은 10분이다. 한편, 이 테스트 시나리오에서는 바닥마찰(bottom friction)이 미치는 영향을 살펴보기 위하여 바닥 마찰이 없는 경우와 마찰이 있는 경우를 각각 테스트하였다.

http://static.apub.kr/journalsite/sites/kso/2019-024-02/N0230240201/images/figure_KSO_24_02_01_F1.jpg
Fig. 1.

Grid design for model scenario 1. (a) is horizontal water depth colormap, (b) is vertical water depth colormap from the south to the north in the center line.

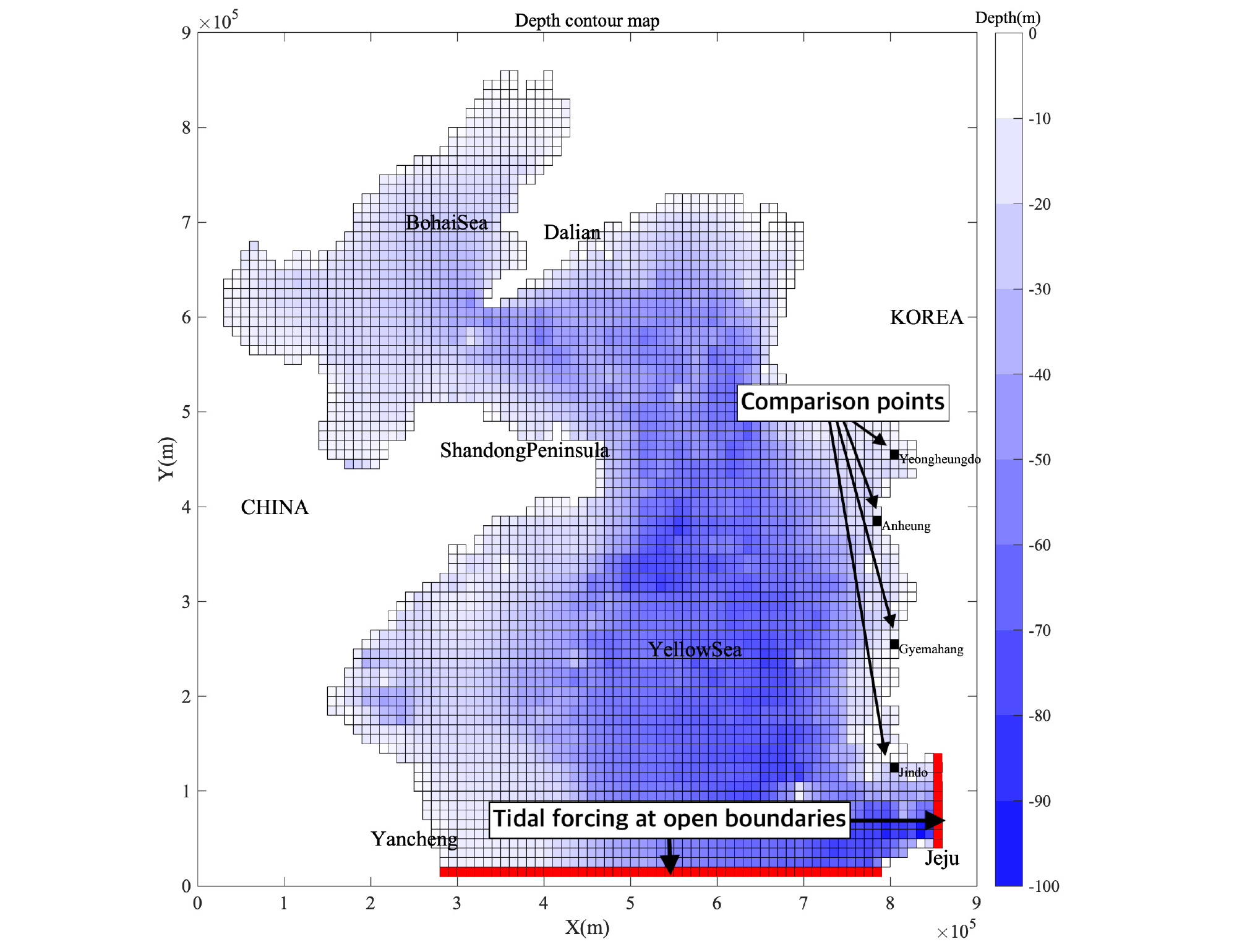
두 번째로, 조석 외력(tidal forcing) 및 전향력(Coriolis force), 난류확산계수로 인한 효과 등을 시험하기 위해 황해(Yellow Sea)를 단순화하여 모델링하였다. x 방향으로 85개, y 방향으로 87개, z 방향으로 13개의 격자를 생성하였고, x, y 방향의 격자 간격은 10 km, z 방향의 격자 간격은 10 m로 구성하였다. 수심은 1/30의 해상도를 가지는 TPX09-ATLAS (OSU Tidal Data Inversion, 2018) 자료를 이용하였다. 경계조건은 남쪽과 동쪽 개방경계를 통한 주요 4대 분조(M2, S2, K1, O1)의 조석 외력이다. 남측 경계의 좌측 시작점은 수심과 같이 TPX09-ATLAS 자료를 이용하였고, 남측 경계의 우측 끝점은 제주도 서부에 위치한 차귀도포구 기본수준점의 조화상수를 이용하였다. 또한, 동쪽 경계의 시작점은 제주도 북부에 위치한 행원포구 기본수준점의 조화상수를, 동측 경계의 끝점은 완도에 위치한 청산도 기본수준점의 조화상수를 이용하였다. TPX09-ATLAS 자료와 기본수준점 자료의 성격이 다르기 때문에 남측 경계의 조화상수는 Table 2와 같이 약간의 보정을 해주었다. 한편, 본 실험의 목적이 황해의 조석을 정확하게 재현하는 것이 아니라 모델의 완성도를 검토하기 위한 것이므로, 모델의 재현성은 위도에 따른 서해 중부와 남부의 조화상수를 대표하는 영흥도, 안흥, 계마항, 진도의 기본수준점 조화상수를 모델 결과와 간략하게 비교하는 것으로 확인하였다. 이 테스트 시나리오의 실험안은 Table 3에 상세하게 제시하였으며, 기본 실험안 1개와 전향력의 적용에 따른 실험안 2개와, 수직 난류확산계수에 따른 실험안 2개로 구성하였다. 계산 시간 간격은 10초이며, 16일간 모의하였고, 결과의 출력 간격은 1시간이다.

Table 2. The raw and adjusted harmonic constants for open boundary forcing

No. tidal constituents South West lon : 120.899999 lat : 32.933335 South East(Chaguido) lon : 126.164722 lat : 33.309167
amplitude (m) Greenwich phase (°) amplitude (m) Greenwich phase (°)
raw adjusted raw adjusted raw adjusted raw adjusted
1 M2 1.107 1.007 46.13 56.13 0.744 0.644 56.93 66.93
2 S2 0.504 0.404 84.31 94.31 0.302 0.202 78.10 88.10
3 K1 0.262 0.312 69.70 79.70 0.243 0.293 87.33 97.33
4 O1 0.153 0.203 41.29 51.29 0.184 0.234 65.41 75.41

Table 3. The model test cases in two scenarios, the simple channel and Yellow Sea

No. Cases Details Open boundary condition
1 Scenario 1 :
simple channel 		Case 1 bottom friction(r) = 0.0 constant source/sink :
10 m3/s
2 Case 2 bottom friction(r) = 0.1
3 Case 3 bottom friction(r) = 0.2
4 Scenario 2 :
simplified Yellow Sea 		Case 1 basic case β-plane
0.0001≦Az≦0.03 		tidal forcing :
M2, S2, K1, O1
5 Case 2 Coriolis
parameter 		f=1×10-4/s
6 Case 3 f=0
7 Case 4 vertical eddy
diffusivity 		0.0001≦Az≦0.01
8 Case 5 0.0001≦Az≦0.06

2.4.1 테스트 모델 1 : 단순 수로(Simple channel)

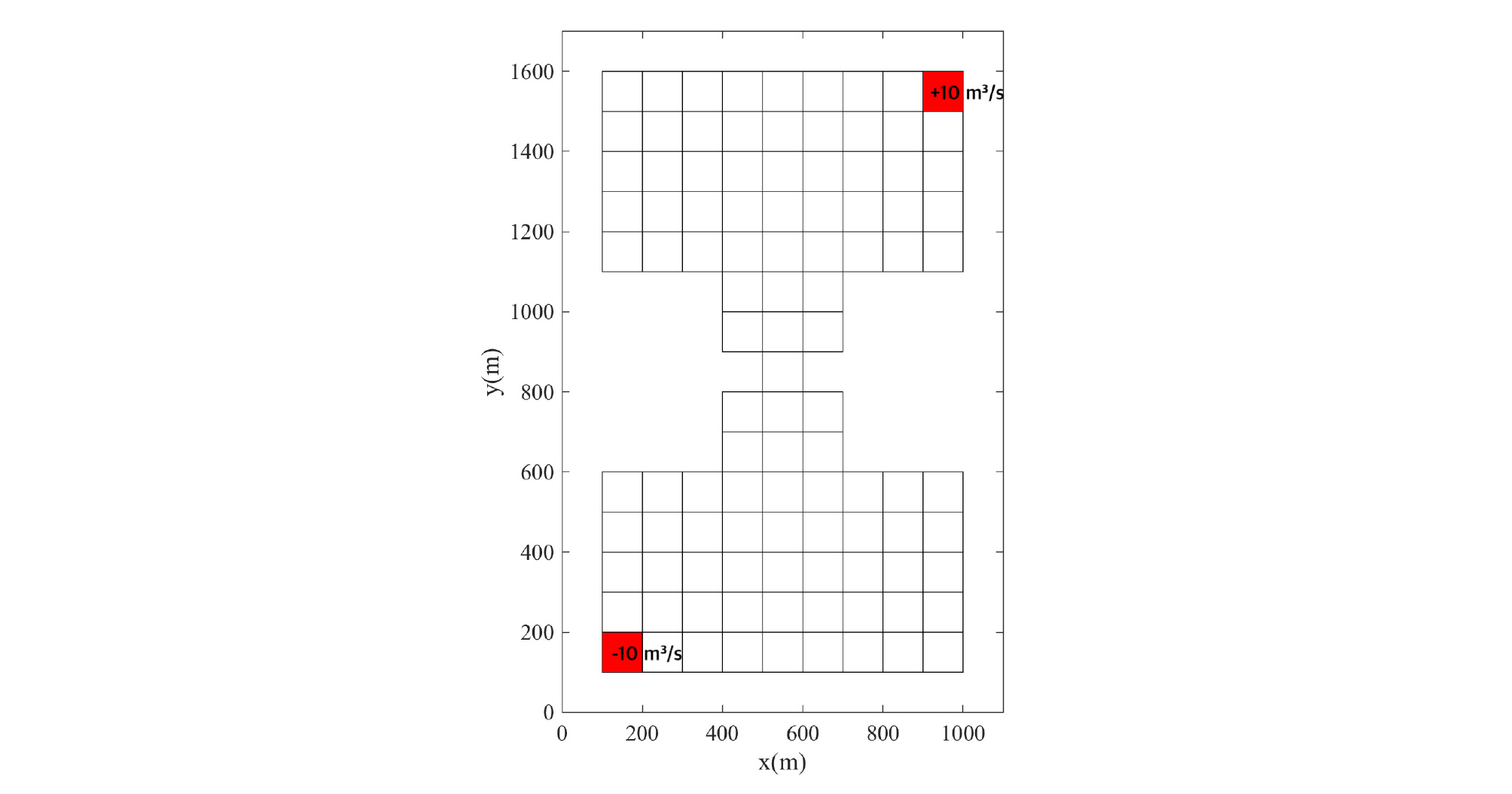
모델 1의 시나리오는 경계 격자에서 일정한 유량이 연속적으로 유입하고, 반대편에서 같은 양의 유량이 연속적으로 빠져나가는 것이다. Fig. 2는 외력이 주어지는 위치를 나타낸다. 모델의 가장 마지막 활성 격자(active cell)에서 10 m3/s 의 유량이 지속적으로 생성되고, 가장 첫 번째 활성 격자에서 같은 양의 유량이 지속적으로 소멸된다. 이 유량은 동수압 q의 변동을 일으키며, 해수의 흐름을 야기한다. 유량의 생성/소멸 항은 다음과 같이 입력된다.

$$Source:-\frac{\partial q_s}{\partial t}=-\rho_sg\;\left(\frac{\partial Q}{\partial x\partial y}\right)$$ (63)
$$Sink:\frac{\partial q_s}{\partial t}=-\rho_sg\;\left(\frac{\partial Q}{\partial x\partial y}\right)$$ (64)
http://static.apub.kr/journalsite/sites/kso/2019-024-02/N0230240201/images/figure_KSO_24_02_01_F2.jpg
Fig.2.

Open boundary forcing cells in scenario 1 with constant flow forcing at two points of each source (+) and sink (-).

한편, 이 테스트의 실험안은 총 3개로, 첫 번째는 해저마찰이 없는 경우, 두 번째는 마찰계수(r)가 0.1인 경우, 셋째는 마찰계수가 0.2인 경우이다.

2.4.2 테스트 모델 2 : 황해(Yellow Sea)

모델 2의 시나리오는 단순화된 황해의 지형을 대상으로 남측과 동측의 개방경계 격자에서 4대 분조 조석이 외력으로 작용하는 것이다. 외력이 주어지는 위치와 관측 값과의 비교 위치는 Fig. 3에 나타냈다. 개방경계의 조석외력은 조석 분조를 입력하는 방식이 아니라 외부 파일로부터 1시간 간격의 조석 변위를 입력받아 계산시간에 대해 보간하여 입력하는 방식을 사용했다. 개방경계는 남측 경계와 동측 경계로 구성하였고, 각 경계의 시작점과 끝점을 보간하여 입력하였다. 외력 조건으로서 조석의 변위는 다음과 같이 생성하여 입력하였다.

$$\eta(t)=\sum_{k=1}^4A_k\cos\;(\omega_kt-P_k)$$ (65)
http://static.apub.kr/journalsite/sites/kso/2019-024-02/N0230240201/images/figure_KSO_24_02_01_F3.jpg
Fig. 3.

Open boundary forcing cells in scenario 2 with tidal forcing at south and east boundaries, and comparison points between observations and computations.

여기서, k는 분조 수, Ak는 각 분조의 진폭, Pk는 위상이며, ωt는 각속도를 뜻한다.

한편, 모델은 난류확산계수에 민감하게 반응하므로 이에 대한 보정이 필요하며, 특히 황해의 경우에는 수직 난류확산계수에 따라 각 분조의 진폭이 크게 달라진다. 또한, 공간적 스케일이 큰 영역을 모델링 할 때에는 전향력을 고려해야 하는데, 이를 감안하여 실험안은 수직 난류확산계수와 전향력의 적용에 따라 크게 두 가지로 나누었다. 먼저 β-plane에 수직 난류확산계수의 최댓값이 0.03인 경우를 기본 실험안으로 두고, 전향력에 대한 추가 실험안으로 첫 번째는 f=1×10-4/s의 경우, 두 번째는 전향력이 없는 경우(f=0)를 각각 실험하였다. 또한 수직 난류확산계수에 대한 실험안으로, 첫 번째는 식 (57)에서 Az의 범위를 0.0001~0.01 m2/s2 범위로 설정한 경우, 두 번째는 0.0001~0.06 m2/s2로 설정한 경우를 각각 실험하였다.

3. 결 과

3.1 테스트 모델 1의 결과

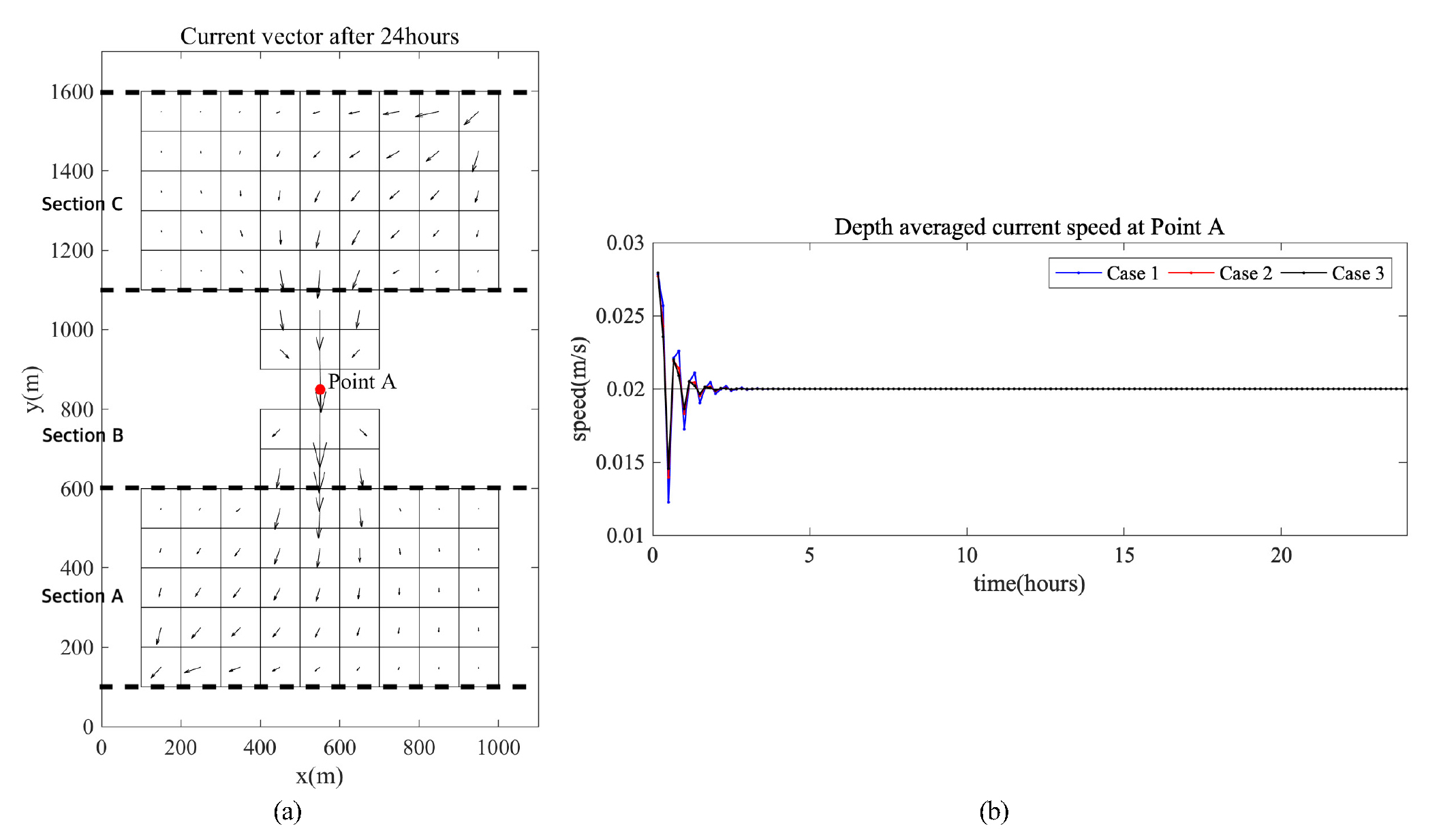
10 m3/s의 유량이 일정하게 생성되고 소멸될 때, Fig. 4의 (a)에 표시한 Point A에서의 유속은 다음과 같이 계산할 수 있다.

$$V_A=\frac Q{A_{i,j-1}}=\frac{10m^3/s}{100m\times5m}=0.02m/s$$ (66)
http://static.apub.kr/journalsite/sites/kso/2019-024-02/N0230240201/images/figure_KSO_24_02_01_F4.jpg
Fig. 4.

The results of scenario 1. (a) is the surface current vector of Case 1 after 24 hours, (b) is the time series of current speed at point A of each test case.

즉, 모델이 정상상태(steady state)에 다다르면, Point A 에서의 유속은 0.02 m/s에 근접해야 하는데, 해저마찰이 있다면 해저에서의 유속은 감소할 것이다. 그러나, 체적이 보존되기 때문에 마찰이 있는 경우에도 수심 평균된 유속은 0.02 m/s에 근접해야 한다. 따라서, 표층에 가까워질수록 유속이 빨라지고, 저층에서는 유속이 느려지기 때문에 수직적인 유속 구배가 발생할 것이다.

각 실험안별 Point A에서의 수심 평균된 유속은 Fig. 4의 (b)에 시계열로 제시하였다. 해저마찰을 고려하지 않은 Case 1의 유속 계산치는 식 (66)의 계산 결과에 정확하게 수렴되었으며, 해저마찰을 고려한 Case 2와 Case 3의 계산 결과도 큰 차이가 없었다. 계산 결과가 정상상태에 도달하는 기간은 5시간 미만이었다. Case 1의 계산 후 약 1일이 지난 시점에서 전체 격자에 대한 표층 유속은 Fig. 4의 (a)에서 확인할 수 있는데, 유량이 발생하는 Section C에서의 유속이 유량이 소멸하는 Section A에서의 유속에 비해 빠른 것을 확인할 수 있다. 이러한 유속의 차이가 발생하는 이유는 각 섹션별로 수심을 다르게 설정하였기 때문이며, Section C의 수심이 Section A의 수심보다 얕으므로, 유속은 더욱 빠르게 나타난다.

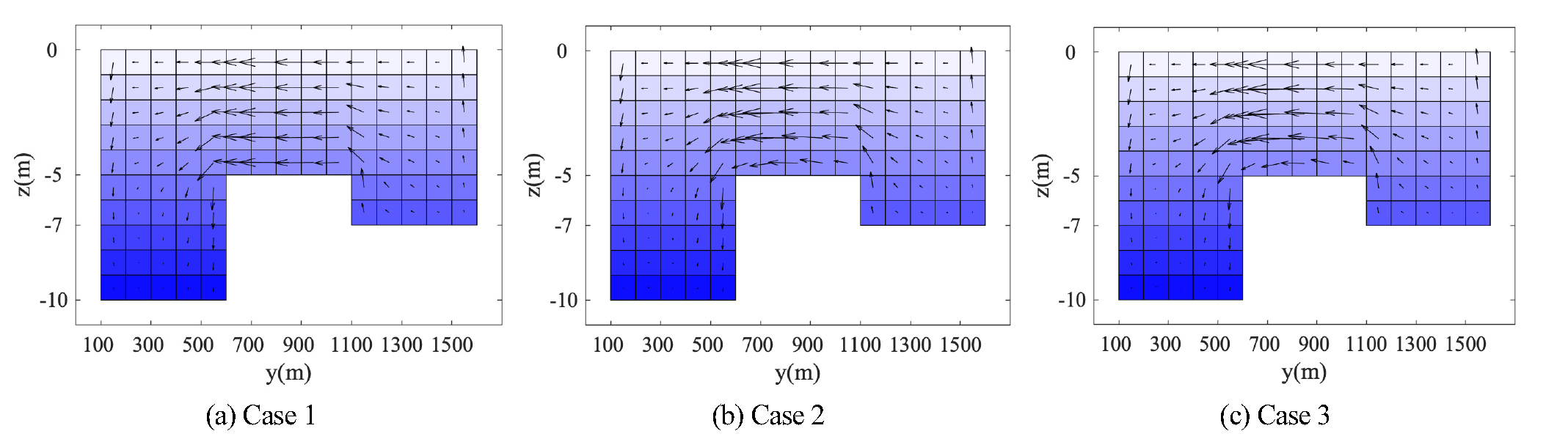
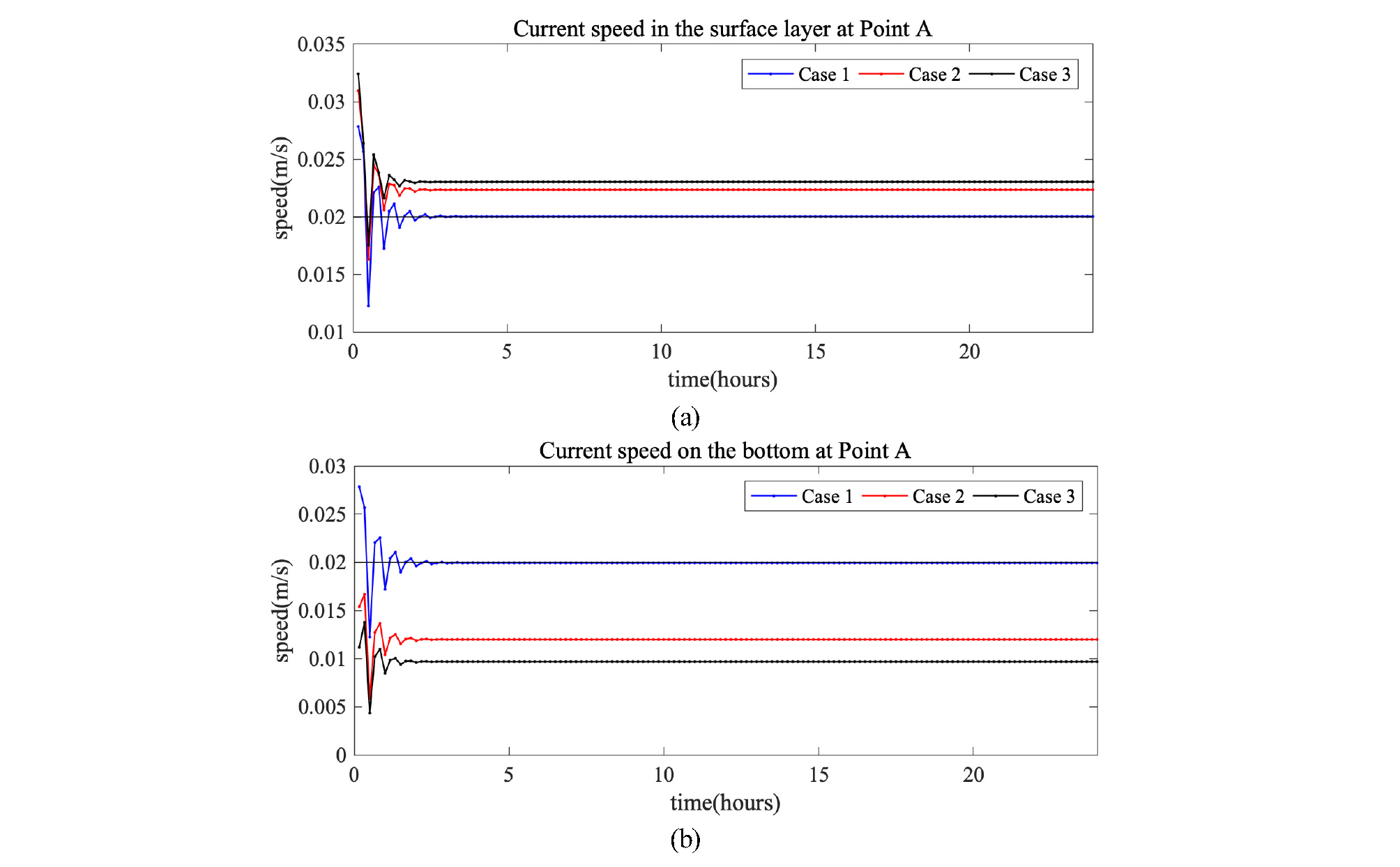
한편, Fig. 5는 실험안별 수직 유속 벡터를 나타낸 것이다. z 방향은 수심을, y 방향은 앞서 Fig. 1에 제시한 바와 같이 남쪽으로부터 북쪽 까지의 거리를 나타낸 것이다. 북쪽 마지막 셀의 표층에서 연직 유속의 벡터가 위쪽으로 나타나고, 남쪽 끝에서 아래로 향하는 것은 물의 흐름이 북쪽에서 남쪽으로 흐르기 때문이다. 연직 유속 벡터의 크기가 비현실적으로 강하게 보이는 것은 수직 스케일이 100배 왜곡되어 있기 때문이며, 실제로 수로의 북쪽 끝부분의 해당 격자에서 수면은 4×10-4 m 만큼 높아진다. Fig. 6은 세 실험안의 Point A에서의 유속을 시계열로 나타낸 것이며, (a)는 표층의 유속을 나타낸 것이고, (b)는 저층 유속을 나타낸 것이다. 해저마찰을 고려하지 않은 Case 1에서는 표층과 저층의 유속이 같으며 이론값인 0.02 m/s에 수렴하고 있다. 그러나, Case 2와 Case 3에서는 표층에서 유속이 0.02 m/s 보다 더 빠르고, 저층에서는 더 느리게 나타난다. 또한 그 차이는 해저마찰계수가 더 큰 Case 3이 Case 2보다 더 크게 나타난다. 물론 앞서 Fig. 4의 (b)에서 확인했듯이 수심 평균된 유속은 모든 실험안에서 0.02 m/s에 수렴하는데, 이는 체적이 보존되기 때문이다.

http://static.apub.kr/journalsite/sites/kso/2019-024-02/N0230240201/images/figure_KSO_24_02_01_F5.jpg
Fig. 5.

The vertical current vectors of three test cases in the center line after 24 hours, (a) is Case 1(r=0), (b) is Case 2(r=0.1), (c) is Case 3(r=0.2).

http://static.apub.kr/journalsite/sites/kso/2019-024-02/N0230240201/images/figure_KSO_24_02_01_F6.jpg
Fig. 6.

The time series of current speed at point A in each test case, (a) is the current speed at the surface layer, (b) is the current speed at the bottom layer.

3.2 테스트 모델 2의 결과

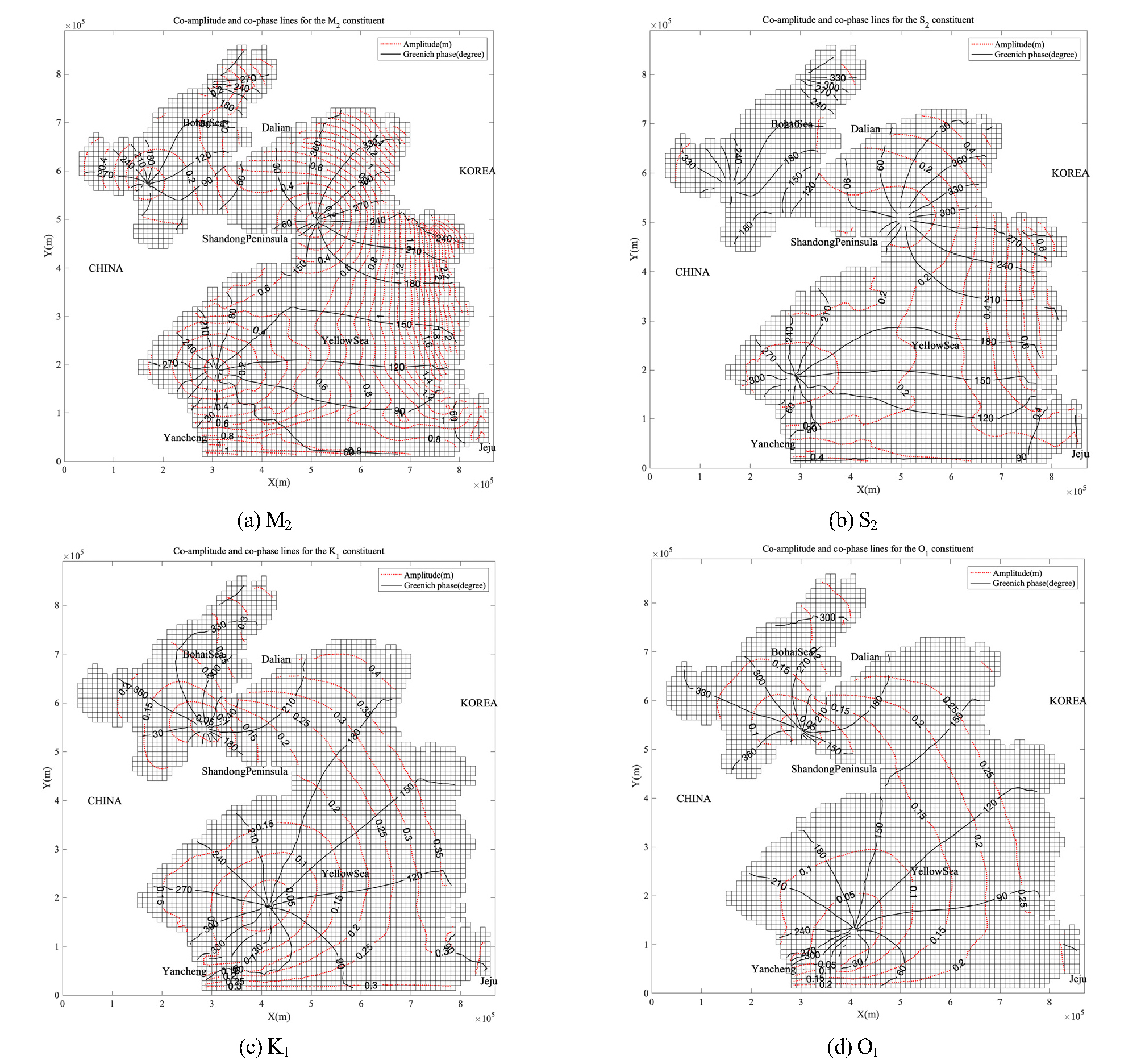
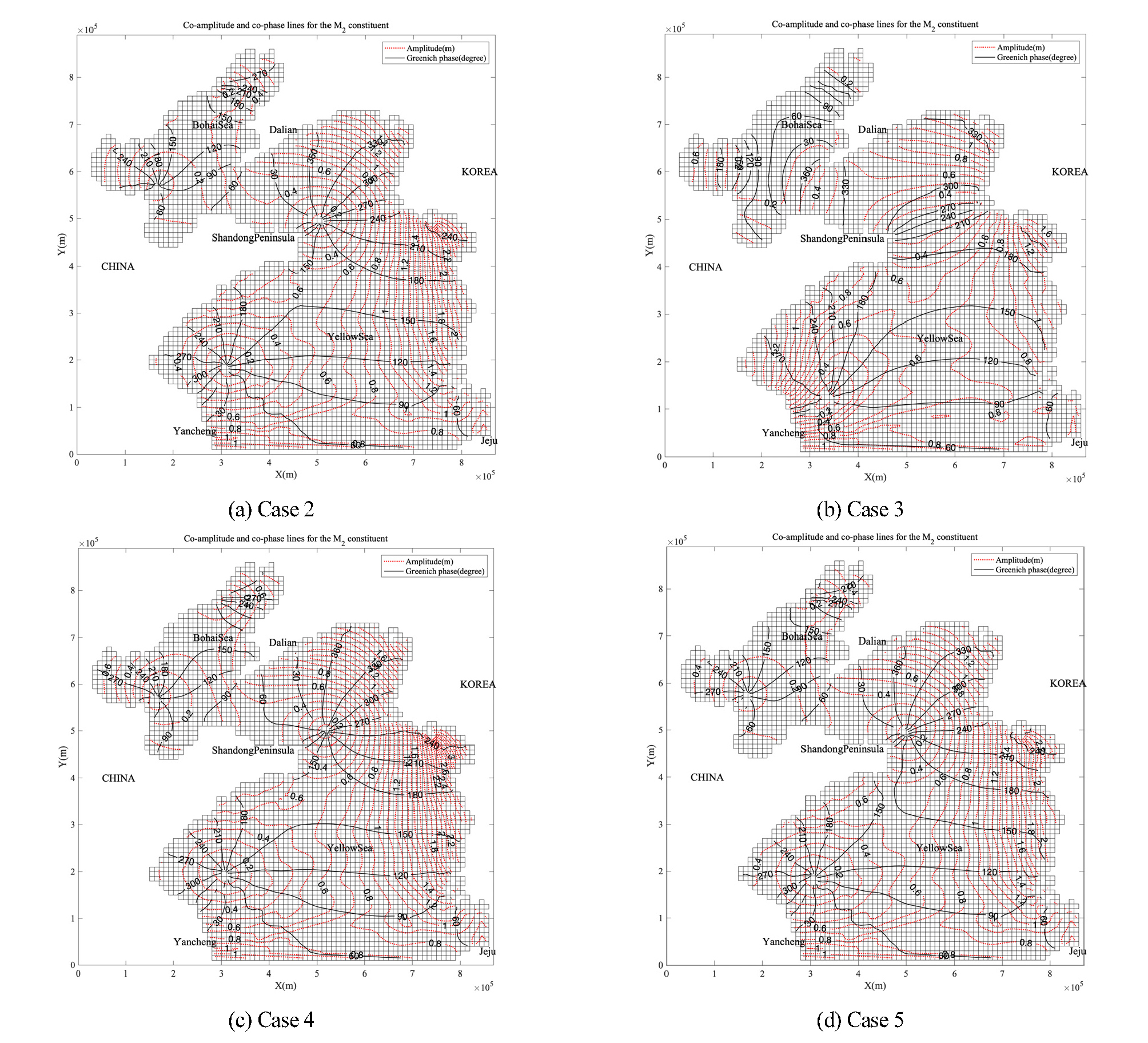
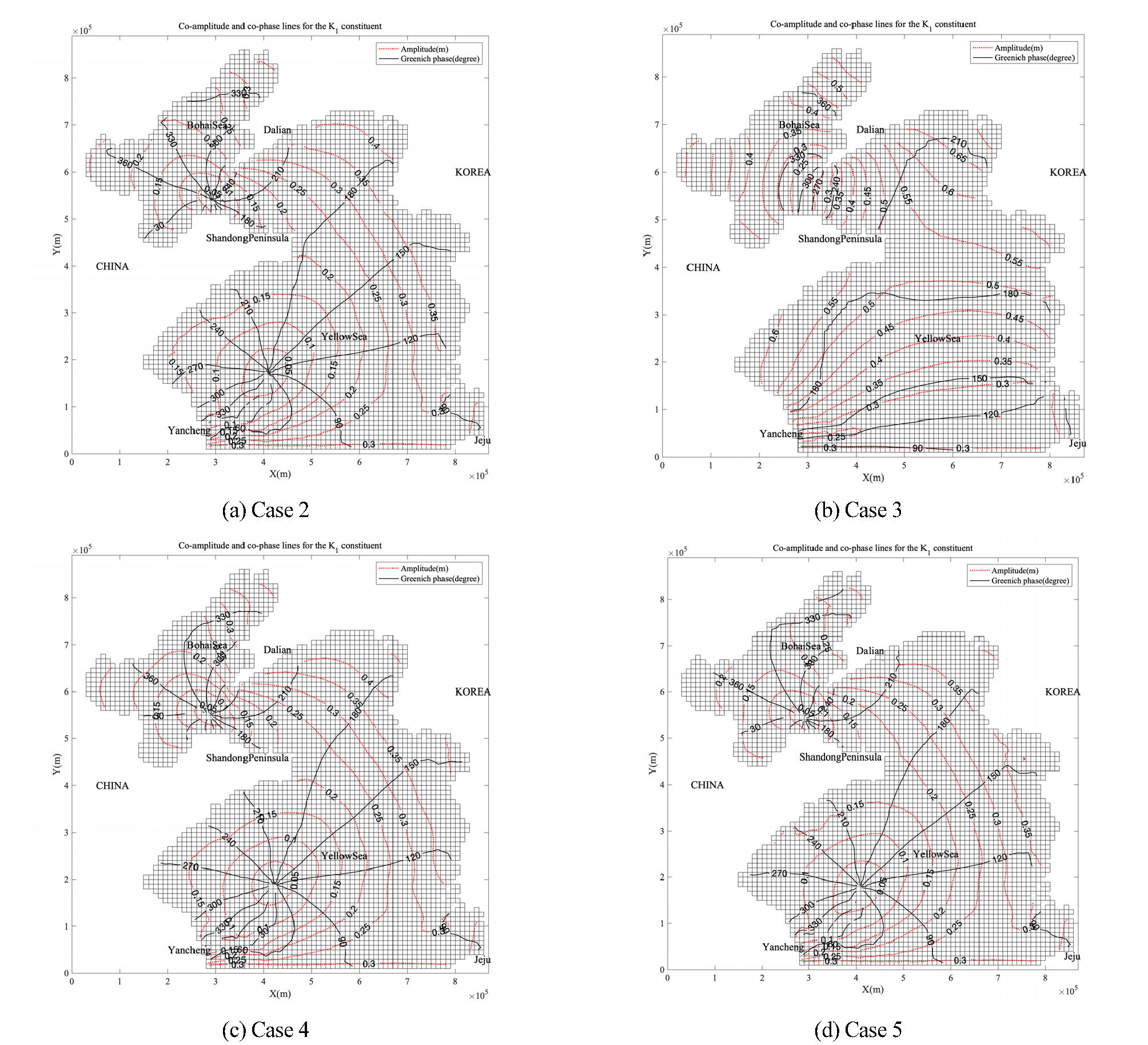
Fig. 7은 두 번째 테스트 모델의 기본 실험안(Case 1)에서 계산된 주요 4대분조의 진폭과 지각을 등고선으로 나타낸 것이다. 그림에서와 같이 황해에서 반일주조 무조점은 4개, 일주조 무조점은 2개로 보인다. 황해의 조석 조화상수를 정확하게 재현해내기 위해서는 더 나은 해상도와 정밀한 수심이 요구되지만, 간단한 테스트 모델을 통해서도 무조점의 위치를 대략적으로 재현해낼 수 있으며, 특히 우리나라 서해안 중부와 남부의 조석 특성을 재현할 수 있다. 결론부터 본다면, Table 4는 각 실험안의 결과가 영흥도, 안흥, 계마항, 진도 기본수준점의 주요 4대 분조 진폭과 지각을 얼마나 잘 재현했는지를 평균 제곱근 오차(RMSE)로 나타낸 것이다. 본 테스트 모델에서는 기본 실험안인 Case 1과 Case 2가 관측 값을 가장 잘 재현하였다. Case 1은 β-plane을 적용하고, 수직 난류확산계수는 0.0001≦Az≦0.03 으로 설정한 것이며, Case 2는 기본 실험안에서 f=1×10-4를 적용한 것이다. 평균 제곱근 오차가 가장 큰 실험안은 Case 3이었는데, 이 실험안은 f=0을 적용한 것으로 전향력을 고려하지 않은 것이다. 또한, Fig. 8과 Fig. 9는 Case 2~Case 5의 M2 분조와 K1 분조의 무조점을 표현한 것인데, Case 3을 제외한 나머지 결과들은 무조점의 위치가 유사하게 나타나지만, 전향력을 고려하지 않은 Case 3은 무조점의 위치가 제대로 재현되지 않았다.

Table 4. The root mean square error for the amplitude and the phase of the 4 major tidal constituents in each case

Cases

Items

 Case 1 Case 2 Case 3 Case 4 Case 5
Amplitude(m) 0.08 0.07 0.49 0.28 0.12
Phase (°) 17.33 17.17 22.72 19.63 16.00

http://static.apub.kr/journalsite/sites/kso/2019-024-02/N0230240201/images/figure_KSO_24_02_01_F7.jpg
Fig. 7.

The tidal co-amplitude and co-phase chart for the 4 major tidal constituents of Case 1. (a) is M2, (b) is S2, (c) is K1, and (d) is O1.

http://static.apub.kr/journalsite/sites/kso/2019-024-02/N0230240201/images/figure_KSO_24_02_01_F8.jpg
Fig. 8.

The tidal co-amplitude and co-phase chart for the M2 tidal constituent of each case. (a) is Case 2(f=1×10-4, (b) is Case 3(f=0), (c) Case 4(Az≦0.001), and (d) is Case 5(Az≦0.01).

http://static.apub.kr/journalsite/sites/kso/2019-024-02/N0230240201/images/figure_KSO_24_02_01_F9.jpg
Fig. 9.

The tidal co-amplitude and co-phase chart for the K1 tidal constituent of each case. (a) is Case 2(f=1×10-4, (b) is Case 3(f=0), (c) Case 4(Az≦0.001), and (d) is Case 5(Az≦0.01).

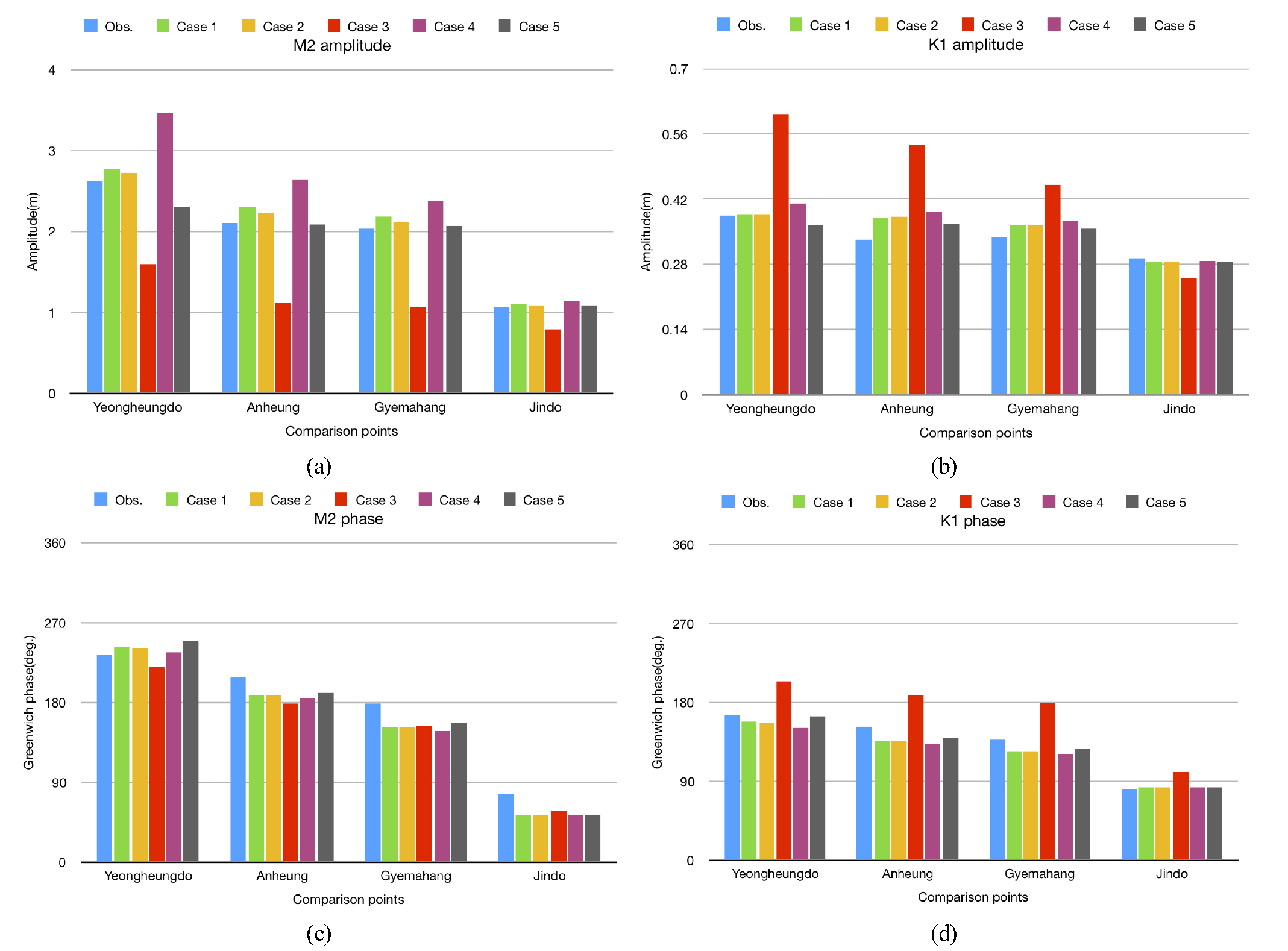
한편, 각 실험안의 결과와 관측 값의 차이를 자세히 살펴보기 위하여, M2 및 K1 분조의 진폭과 지각을 직접적으로 비교하여 Fig. 10에 제시하였다. 먼저 Case 1과 Case 2의 결과는 서로 유사하게 나타났고, 관측 값과도 큰 차이가 없었다. Case 3(f=0)의 경우에는 M2 분조의 진폭이 너무 작게 계산되었고 K1 분조의 진폭은 너무 크게 계산되었으며, K1 분조의 지각도 차이가 크게 나타났다. Case 4(0.0001≦Az≦0.01)는 M2 분조의 진폭이 너무 크게 계산되었으며, Case 5(0.0001≦Az≦0.06)는 인천 영흥도에서의 M2 분조 진폭이 너무 작게 계산되었다. Case 4와 Case 5의 결과로 미루어 수직 난류확산계수를 조정하는 것으로 모델의 정확도를 향상시킬 수 있다는 것을 알 수 있다.

http://static.apub.kr/journalsite/sites/kso/2019-024-02/N0230240201/images/figure_KSO_24_02_01_F10.jpg
Fig. 10.

The comparison of amplitude and phase of M2, K1 constituent for each case. (a) is M2 amplitude, (b) is K1 amplitude, (c) is M2 phase, and (d) is K1 phase.

4. 결 론

본 연구에서는 적시 컴파일 언어인 줄리아를 이용하여 포트란 등의 고전적인 컴파일 언어에 필적하는 성능을 가진 고성능 해양모델을 개발하고자 하였다. 먼저, 비압축성 유체에 대한 나비에-스톡스 식의 수치해법을 줄리아 코드로 작성하였고, 줄리아 계산 코드를 시험하기 위하여 두 가지의 모델을 구축하였다. 첫 번째로, 일정한 유량의 생성/소멸(source/sink) 조건을 시험하기 위해 단순한 수로 형태를 모델링하였고, 두 번째로, 조석 외력(tidal forcing) 및 전향력(Coriolis force), 난류확산계수로 인한 효과 등을 시험하기 위해 황해(Yellow Sea)를 단순화하여 모델링하였다.

1) 시나리오 1은 일정한 유량이 생성/소멸되는 조건을 모델링 한 것으로, 해저마찰계수의 크기에 따라 3개의 실험안을 테스트하였다.

2) 3개의 실험안에서 수심 평균된 유속은 이론값에 수렴하였으며, 해저마찰계수가 커질수록 수직적인 유속 구배가 커졌다.

3) 시나리오 2는 조석 변위를 외력으로 모델링 한 것으로, 단순화된 황해를 대상으로 하였으며, 전향력과 수직 난류확산계수의 크기에 따라 총 5개의 실험안을 테스트하였다.

4) Case 1은 β-plane을 적용하고, 수직 난류확산계수는 0.0001≦Az≦0.03으로 설정한 것이며, Case 2는 기본 실험안에서 f=1×10-4를 적용한 것인데, 이 두가지 실험안이 관측 값을 가장 잘 재현하였다.

5) f=0을 적용한 Case 3에서 평균 제곱근 오차가 가장 크게 나타났고, 무조점 위치가 제대로 재현되지 않았다.

6) M2 및 K1 분조의 진폭과 지각을 직접적으로 비교한 결과, Case 4(0.0001≦Az≦0.01)는 M2 분조의 진폭이 너무 크게 계산되었으며, Case 5(0.0001≦Az≦0.06)는 인천에서의 M2 분조 진폭이 너무 작게 계산되었다.

7) 따라서, Case 4와 Case 5의 결과로 미루어 수직 난류확산계수를 조정하는 것으로 모델의 정확도를 향상시킬 수 있다는 것을 알 수 있었다.

8) 두 가지 시나리오에 포함된 총 8개의 실험안을 테스트한 결과, 줄리아 언어를 이용한 해양모델의 개발이 성공적으로 이루어졌다고 판단된다.

Acknowledgements

세심한 검토와 유익한 의견으로 본 논문의 질이 크게 향상되는데 도움을 주신 익명의 심사위원 분들께 진심으로 감사드립니다.

References

1
Arakawa, A. and V.R. Lamb, 1977. Computational Design of the Basic Dynamical Processes of the UCLA General Circulation Model, Methods in Computational Physics: Advances in Research and Applications, 17: 173-265.
10.1016/B978-0-12-460817-7.50009-4
2
Aycock, 2003. 2. JIT Compilation Techniques, 2.1 Genesis, p. 98.
3
Brunt, D., 1927. The period of simple vertical oscillations in the atmosphere. Quarterly Journal of the Royal Meteorological Society, 53(221): 30-32.
10.1002/qj.49705322103
4
Fringer, O.B., S.W. Armfield and R. L. Street., 2005. Reducing numerical diffusion in interfacial gravity wave simulations. International Journal for Numerical Methods in Fluids, 49: 301-329.
10.1002/fld.993
5
GitHub, Inc., 2018, GitHub, Retrieved from https://github.com/
6
Hamrick, J.M., 1992. A three-dimensional environmental fluid dynamics computer code : Theoretical and computational aspects, The College of William and Mary, Virginia Institute of Marine Science, Special Report 317, VA. pp. 1-63.
7
JuliaLang., 2018a. Julia 1.0 Documentation, Retrieved from https://docs.julialang.org/en/v1/.
8
JuliaLang., 2018b. The Julia Language, Retrieved from https://github.com/JuliaLang/julia.
9
Kämpf, J., 2009. Ocean Modelling for Beginners (using open-source software), Springer, p. 59.
10.1007/978-3-642-00820-7
10
Kämpf, J., 2010. Advanced Ocean Modelling (using open-source software), Springer.
10.1007/978-3-642-10610-1
11
Kochergin, V. P., 1987. Three-dimensional prognostic models. In: Heaps, N. S. (ed.), Three- Dimensional Coastal Ocean Models, Coastal Estuarine Science Series, vol. 4, Union, American Geophysical Washington, DC, pp. 201-208.
10.1029/CO004p0201
12
Lattner, C., 2002. LLVM: An Infrastructure for Mulit-Stage Optimization, Masters Thesis, Computer Science Dept., University of Illinois at Urbana-Champaign, Dec.
13
MathWorks, 2018. MATLAB, Retrieved from http://www.mathworks.com/.
14
McCarthy, J., 1960. Recursive Functions of Symbolic Expressions and Their Computation by Machine, Part I, Communications of the ACM, April, 3(4): 184-195.
10.1145/367177.367199
15
OSU Tidal Data Inversion, 2018. TPX09-ATLAS, Retrieved from http://volkov.oce.orst.edu/tides/tpxo9_atlas.html.
16
Poisson, S.-D., 1813. Remarques sur une équation qui se présente dans a théorie des attractions des sphéroides, Nouvelle Bulletin de la Société Philomatique, 3: 388-392.
17
Python Software Foundation, 2018. Python, Retrieved from https://www.python.org/.
18
Smagorinsky, J., 1963. General circulation experiments with the primitive equations - I. The basic experiment. Mon. Weather Rev., 91: 99-165.
10.1175/1520-0493(1963)091<0099:GCEWTP>2.3.CO;2
19
The R Foundation, 2018. R, Retrieved from https://www.r-project.org/.
20
Väisälä, V., 1925. Über die Wirkung der Windschwankungen aufdie Pilotbeobachtungen. Soc. Sci. Fenn. Commentat. Phys.-Math., 2(19): 1-46.
페이지 상단으로 이동하기